题目内容
11.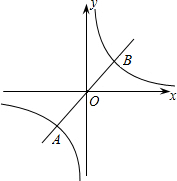 如图,已知正比例函数y=2x和反比例函数y=$\frac{k}{x}$(k≠0)的图象交于A、B两点,若A点的纵坐标为-2.
如图,已知正比例函数y=2x和反比例函数y=$\frac{k}{x}$(k≠0)的图象交于A、B两点,若A点的纵坐标为-2.(1)求反比例函数的解析式和点B坐标;
(2)根据图象,直接写出正比例函数值大于反比例函数值时自变量x的取值范围;
(3)若C是双曲线上的动点,D是x轴上的动点,是否存在这样的点C和点D,使以A、B、CD为顶点的四边形是平行四边形?若存在,求出C、D坐标;若不存在,请说明理由.
分析 (1)把y=-2代入y=2x中求出x的值,确定出A坐标,利用对称性确定出B坐标,把A点坐标代入反比例解析式求出k的值,即可确定出反比例解析式;
(2)以A,B的横坐标及0,把x轴分为四个范围,找出正比例函数图象位于反比例函数图象上方时x的范围即可;
(3)存在这样的点C和点D,使以A、B、C、D为顶点的四边形是平行四边形,如图所示,分两种情况考虑:(i)根据平移规律及AC∥BD,AC=BD得:点B先向下平移两个单位,则A也向下平移两个单位,得出C的纵坐标,代入反比例解析式求出C横坐标,确定出C坐标,得到A平移到C的路径,进而确定出B平移到D的路径,求出D坐标;(ii)同理得到C′与D′坐标即可.
解答 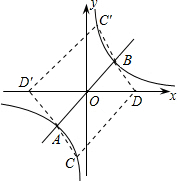 解:(1)把y=-2代入y=2x得:x=-1,即A(-1,-2),
解:(1)把y=-2代入y=2x得:x=-1,即A(-1,-2),
由对称性得:B(1,2),
把A(-1,-2)代入反比例解析式得:k=2,
则反比例解析式为y=$\frac{2}{x}$,B(1,2);
(2)由图象得:-1<x<0或x>1时,正比例函数值大于反比例函数值;
(3)存在这样的点C和点D,使以A、B、CD为顶点的四边形是平行四边形,
如图所示,分两种情况考虑:
(i)根据平移规律及AC∥BD,AC=BD得:点B先向下平移两个单位,则A也向下平移两个单位,
∴C纵坐标为为-4,
把y=-4代入反比例解析式得:x=-$\frac{1}{2}$,即C(-$\frac{1}{2}$,-4),即C是由A先向下平移两个单位,再向左平移$\frac{1}{2}$个单位,
∴D是由B先向下平移两个单位,再向左平移$\frac{1}{2}$个单位,即D($\frac{3}{2}$,0);
(ii)同理C′($\frac{1}{2}$,4),D′(-$\frac{3}{2}$,0),
综上,存在这样的点C和点D,使以A、B、CD为顶点的四边形是平行四边形,此时C(-$\frac{1}{2}$,-4)、D($\frac{3}{2}$,0)或C($\frac{1}{2}$,4)、D(-$\frac{3}{2}$,0).
点评 此题属于反比例函数综合题,涉及的知识有:坐标与图形性质,一次函数与反比例函数的交点坐标,以及平移的性质,利用了数形结合及分类讨论的思想,熟练掌握平移的性质是解本题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | c<a<b | B. | b<a<c | C. | a<b<c | D. | c<b<a |
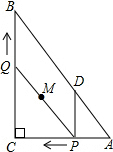 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,动点P从点A开始沿边AC向点C以每秒1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD∥BC,交AB于点D,连接PQ.点P,Q分别从点A,C同时出发,当其中一点到达终点时,另一点也随之停止运动,设运动时间为t秒(t>0).
如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,动点P从点A开始沿边AC向点C以每秒1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD∥BC,交AB于点D,连接PQ.点P,Q分别从点A,C同时出发,当其中一点到达终点时,另一点也随之停止运动,设运动时间为t秒(t>0).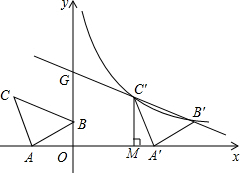 如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(-2,0)、B(0,d)、C(-3,2).
如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(-2,0)、B(0,d)、C(-3,2).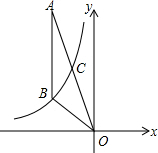 如图,反比例函数y=$\frac{k}{x}$(x<0)经过△OAB的顶点B和线段OA的中点C,AB∥y轴,点B的坐标为(-3,2).
如图,反比例函数y=$\frac{k}{x}$(x<0)经过△OAB的顶点B和线段OA的中点C,AB∥y轴,点B的坐标为(-3,2).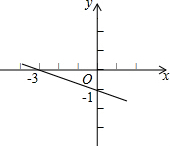 如图,图中直线l的解析式是y=-$\frac{1}{3}$x-1.
如图,图中直线l的解析式是y=-$\frac{1}{3}$x-1.