题目内容
10.甲仓库有水泥110吨,乙仓库有水泥70吨,现要将这些水泥全部运往A,B两工地,调运任务承包给某运输公司.已知A工地需水泥100吨,B工地需水泥80吨,从甲仓库运往A,B两工地的路程和每吨每千米的运费如表:| 路程(千米) | 运费(元/吨.千米) | |||
| 甲仓库 | 乙仓库 | 甲仓库 | 乙仓库 | |
| A地 | 25 | 20 | 1 | 0.8 |
| B地 | 20 | 15 | 1.2 | 1.2 |
(2)求总运费W关于x的函数关系式,并求出自变量的取值范围;
(3)当甲、乙两仓库各运往A,B两工地多少吨水泥时,总运费最省?最省的总运费是多少?
分析 (1)根据甲仓库运往A地水泥吨数结合甲仓水泥的总吨数即可得出甲仓库运往B地水泥吨数,由A地需要水泥的吨数减去甲仓库运往A地水泥吨数即可得出乙仓库运往A地水泥吨数,再根据B地水泥需要的吨数减去甲仓库运往B地水泥吨数即可得出乙仓库运往B地水泥吨数;
(2)根据总运费=甲仓运往A地水泥的运费+甲仓运往B地水泥的运费+乙仓运往A地水泥的运费+乙仓运往B地水泥的运费即可得出W关于x的函数关系式,再由A、B两地需要的水泥吨数即可得出关于x的一元一次不等式组,解之即可得出自变量x的取值范围;
(3)根据(2)的函数关系式利用一次函数的性质即可解决最值问题.
解答 解:(1)设甲仓库运往A地水泥x吨,则甲仓库运往B地水泥(110-x)吨,乙仓库运往A地水泥(100-x)吨,乙仓库运往B地水泥80-(110-x)=x-30吨.
故答案为:110-x;100-x;x-30.
(2)根据题意得:W=1×25x+1.2×20(110-x)+0.8×20(100-x)+1.2×15(x-30)=3x+3700.
∵$\left\{\begin{array}{l}{x≤100}\\{110-x≤80}\end{array}\right.$,
∴30≤x≤100.
∴总运费W关于x的函数关系式为W=3x+3700(30≤x≤100).
(3)∵在W=3x+3700中k=3>0,
∴W随着x的增加而增加,
∴当x=30时,W取最小值,最小值为3790,
∴110-x=80,100-x=70;x-30=0.
答:当甲仓库运往A地水泥30吨、运往B地水泥80吨、乙仓库运往A地水泥70吨、运往B地水泥0吨时,总运费最省,最省的总运费是3790元.
点评 本题考查了一次函数的应用、一次函数的性质、列代数式以及解一元一次不等式组,解题的关键是:(1)根据数量关系列出代数式;(2)根据总运费=甲仓运往A地水泥的运费+甲仓运往B地水泥的运费+乙仓运往A地水泥的运费+乙仓运往B地水泥的运费找出W关于x的函数关系式;(3)根据一次函数的单调性解决最值问题.

 阅读快车系列答案
阅读快车系列答案| A. | a>b | B. | -$\frac{1}{2}$a<-$\frac{1}{2}$b | C. | 2a+3>2b+3 | D. | -7a>-7b |
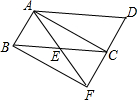 如图,已知点E是?ABCD中BC边的中点,连接AE并延长交DC的延长线于点F.
如图,已知点E是?ABCD中BC边的中点,连接AE并延长交DC的延长线于点F.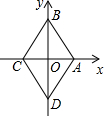 菱形ABCD在直角坐标系中的位置如图所示,其中点A的坐标为(1,0),点B的坐标为(0,$\sqrt{3}$),动点P从点A出发,沿A→B→C→D→A→B→…的路径,在菱形的边上以每秒1个单位长度的速度移动,移动到第2015秒时,点P的坐标为( $\frac{3}{4}$,-$\frac{\sqrt{3}}{4}$).
菱形ABCD在直角坐标系中的位置如图所示,其中点A的坐标为(1,0),点B的坐标为(0,$\sqrt{3}$),动点P从点A出发,沿A→B→C→D→A→B→…的路径,在菱形的边上以每秒1个单位长度的速度移动,移动到第2015秒时,点P的坐标为( $\frac{3}{4}$,-$\frac{\sqrt{3}}{4}$).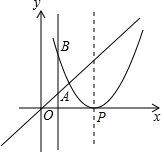 己知抛物线y=(x-2)2,P是抛物线对称轴上的一个点,直线x=t分别与直线y=x、抛物线交于点A,B,若△ABP是等腰直角三角形,则t的值为0或3或$2±\sqrt{2}$或$3±\sqrt{3}$或$\frac{{7±\sqrt{17}}}{2}$.
己知抛物线y=(x-2)2,P是抛物线对称轴上的一个点,直线x=t分别与直线y=x、抛物线交于点A,B,若△ABP是等腰直角三角形,则t的值为0或3或$2±\sqrt{2}$或$3±\sqrt{3}$或$\frac{{7±\sqrt{17}}}{2}$.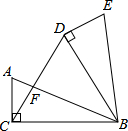 如图所示,在△ABC=90°,AC=5cm,BC=12cm,将△ABC绕点B顺时针旋转60°,得到△BDE,连接DC交AB于点F.
如图所示,在△ABC=90°,AC=5cm,BC=12cm,将△ABC绕点B顺时针旋转60°,得到△BDE,连接DC交AB于点F.