题目内容
2.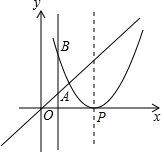 己知抛物线y=(x-2)2,P是抛物线对称轴上的一个点,直线x=t分别与直线y=x、抛物线交于点A,B,若△ABP是等腰直角三角形,则t的值为0或3或$2±\sqrt{2}$或$3±\sqrt{3}$或$\frac{{7±\sqrt{17}}}{2}$.
己知抛物线y=(x-2)2,P是抛物线对称轴上的一个点,直线x=t分别与直线y=x、抛物线交于点A,B,若△ABP是等腰直角三角形,则t的值为0或3或$2±\sqrt{2}$或$3±\sqrt{3}$或$\frac{{7±\sqrt{17}}}{2}$.
分析 首先求出抛物线与直线y=x的交点坐标,再分四种情形列出方程即可解决问题.
解答 解:由$\left\{\begin{array}{l}{y=x}\\{y=(x-2)^{2}}\end{array}\right.$解得$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$或$\left\{\begin{array}{l}{x=4}\\{y=4}\end{array}\right.$,
根据的通知解三角形的性质可知当AB=|Px-Ax|或AB=2|Px-Ax|时,△PAB可以是等腰直角三角形.
①当0<x≤1时,(t-2)2-t=2-t或(t-2)2-t=2(2-t),
解得t=2-$\sqrt{2}$或0,
②当1<t≤2时,t-(t-2)2=2-t或t-(t-2)2=2(2-t),
解得t=3-$\sqrt{3}$或$\frac{7-\sqrt{17}}{2}$,
③当2<t≤4时,t-(t-2)2=(t-2),或t-(t-2)2=2(t-2),
解得t=2+$\sqrt{2}$或3,
④当t>4时,(t-2)2-t=t-2或(t-2)2-t=2(t-2),
解得t=3+$\sqrt{3}$或$\frac{7+\sqrt{17}}{2}$,
综上所述,满足条件的t的值为0或3或$2±\sqrt{2}$或$3±\sqrt{3}$或$\frac{{7±\sqrt{17}}}{2}$.
故答案为0或3或$2±\sqrt{2}$或$3±\sqrt{3}$或$\frac{{7±\sqrt{17}}}{2}$.
点评 本题考查二次函数的性质、一次函数的应用、等腰直角三角形的性质、一元二次方程等知识,解题的关键是学会用转化的思想思考问题,学会构建方程解决问题,属于中考填空题中的压轴题.

| 路程(千米) | 运费(元/吨.千米) | |||
| 甲仓库 | 乙仓库 | 甲仓库 | 乙仓库 | |
| A地 | 25 | 20 | 1 | 0.8 |
| B地 | 20 | 15 | 1.2 | 1.2 |
(2)求总运费W关于x的函数关系式,并求出自变量的取值范围;
(3)当甲、乙两仓库各运往A,B两工地多少吨水泥时,总运费最省?最省的总运费是多少?
 如图,有一条小路穿过长方形的草地ABCD,若AB=60m,BC=84m,AE=100m,AE∥CF,则这条小路AECF的面积是多少?
如图,有一条小路穿过长方形的草地ABCD,若AB=60m,BC=84m,AE=100m,AE∥CF,则这条小路AECF的面积是多少? 如图,A是斜边长为m的等腰直角三角形,B,C,D都是正方形.则A,B,C,D的面积的和等于$\frac{9}{4}$m2.
如图,A是斜边长为m的等腰直角三角形,B,C,D都是正方形.则A,B,C,D的面积的和等于$\frac{9}{4}$m2.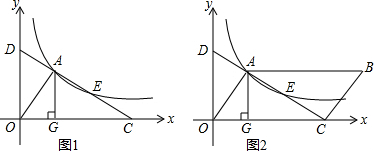

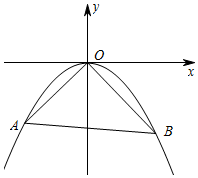 如图,直线y=kx+b(b<0)与抛物线y=ax2相交于点A(x1,y1),B(x2,y2)两点,抛物线y=ax2经过点(4,-2)
如图,直线y=kx+b(b<0)与抛物线y=ax2相交于点A(x1,y1),B(x2,y2)两点,抛物线y=ax2经过点(4,-2)