题目内容
18.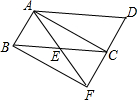 如图,已知点E是?ABCD中BC边的中点,连接AE并延长交DC的延长线于点F.
如图,已知点E是?ABCD中BC边的中点,连接AE并延长交DC的延长线于点F.(1)连按AC,BF,若∠AEC=2∠ABC,求证:四边形ABFC为矩形;
(2)在(1)的条件下,若△AFD是等边三角形,且边长为4,求四边形ABFC的面积.
分析 (1)由ABCD为平行四边形,根据平行四边形的对边平行得到AB与DC平行,根据两直线平行内错角相等得到一对角相等,由E为BC的中点,得到两条线段相等,再由对应角相等,利用ASA可得出三角形ABE与三角形FCE全等;进而得出AB=FC,即可得出四边形ABFC是平行四边形,再由直角三角形的判定方法得出△BFC是直角三角形,即可得出平行四边形ABFC是矩形.
(4)由等边三角形的性质得出∠AFC=60°,AF=DF=4,得出CF=CD=2,由矩形的性质得出∠ACF=90°,得出AC=$\sqrt{3}$CF=2$\sqrt{3}$,即可得出四边形ABFC的面积=AC•CF=4$\sqrt{3}$.
解答 (1)证明:∵四边形ABCD为平行四边形,
∴AB∥DC,
∴∠ABE=∠ECF,
又∵E为BC的中点
∴BE=CE,
在△ABE和△FCE中,$\left\{\begin{array}{l}{∠ABE=∠ECF}&{\;}\\{BE=CF}&{\;}\\{∠AEB=∠FEC}&{\;}\end{array}\right.$,
∴△ABE≌△FCE(ASA);
∴AE=EF,AB=CF,
∴四边形ABFC是平行四边形,
∵∠AEC=2∠ABC=∠ABC+∠BAE,
∴∠ABC=BAE,
∴AE=BE
∵AE=EF,BE=CE,
∴AF=BC
∴平行四边形ABFC是矩形.
(2)解:∵△AFD是等边三角形,
∴∠AFC=60°,AF=DF=4,
∴CF=CD=2,
∵四边形ABFC是矩形,
∴∠ACF=90°,
∴AC=$\sqrt{3}$CF=2$\sqrt{3}$,
∴四边形ABFC的面积=AC•CF=4$\sqrt{3}$.
点评 此题主要考查了矩形的判定以及全等三角形的判定与性质等知识,根据已知得出AB=CF是解题关键.

 阅读快车系列答案
阅读快车系列答案| A. | 小王合算 | B. | 小李合算 | ||
| C. | 一样合算 | D. | 无法确定谁更合算 |
| 运行区间 | 公布票价 | 学生票 | ||
| 上车站 | 下车站 | 一等座 | 二等座 | 二等座 |
| 长沙 | 井冈山 | 81(元) | 68(元) | 51(元) |
(2)由于各种原因,二等座火车票单程只能买x张(x小于参加社会实践的人数),其余的须买一等座火车票,在保证每位参与人员都有座位坐的前提下,请你设计最经济的购票方案,并写出购买火车票的总费用(单程)y与x之间的函数关系式.
| 路程(千米) | 运费(元/吨.千米) | |||
| 甲仓库 | 乙仓库 | 甲仓库 | 乙仓库 | |
| A地 | 25 | 20 | 1 | 0.8 |
| B地 | 20 | 15 | 1.2 | 1.2 |
(2)求总运费W关于x的函数关系式,并求出自变量的取值范围;
(3)当甲、乙两仓库各运往A,B两工地多少吨水泥时,总运费最省?最省的总运费是多少?
 如图,有一条小路穿过长方形的草地ABCD,若AB=60m,BC=84m,AE=100m,AE∥CF,则这条小路AECF的面积是多少?
如图,有一条小路穿过长方形的草地ABCD,若AB=60m,BC=84m,AE=100m,AE∥CF,则这条小路AECF的面积是多少?
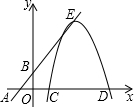 如图,一次函数y=x+2与x轴交于点A,与y轴交于点B,一抛物线的顶点在直线AB上,形状与函数y=-$\frac{1}{2}$x2图象相同,它与x轴分别交于点C、D(点C在点D的左侧),抛物线的顶点为点E.
如图,一次函数y=x+2与x轴交于点A,与y轴交于点B,一抛物线的顶点在直线AB上,形状与函数y=-$\frac{1}{2}$x2图象相同,它与x轴分别交于点C、D(点C在点D的左侧),抛物线的顶点为点E.