题目内容
1.函数y=$\frac{1}{1-x(1-x)}$的最大值是$\frac{4}{3}$.分析 确定y=$\frac{1}{1-x(1-x)}$ 最大值就是确定1-x(1-x)的最小值.
解答 解:∵y′=1-x(1-x)=x2-x+1=(x-$\frac{1}{2}$)2+$\frac{3}{4}$,
∴有最小值$\frac{3}{4}$,
∴y=$\frac{1}{1-x(1-x)}$的最大值是$\frac{1}{\frac{3}{4}}$=$\frac{4}{3}$.
故答案为:$\frac{4}{3}$.
点评 本题考查了二次函数的最值,解题的关键是能够确定分母的最小值,从而确定整个函数的最大值,难度不大.

练习册系列答案
相关题目
2.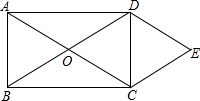 如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.
如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.
(1)若AB=6,BC=8,求四边形OCED的面积.
(2)若∠ACB=30°,菱形OCED的面积为18$\sqrt{3}$,求AC的长.
 如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.
如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.(1)若AB=6,BC=8,求四边形OCED的面积.
(2)若∠ACB=30°,菱形OCED的面积为18$\sqrt{3}$,求AC的长.
9.长沙某校准备组织学生及学生家长到井冈山进行社会实践,为了便于管理,所有人员必须乘坐在同一列火车上;根据报名人数,若都买一等座单程火车票需17010元,若都买二等座单程火车票且花钱最少,则需11220元;已知学生家长与教师的人数之比为2:1,长沙到井冈山的火车票价格(部分)如下表所示:
(1)参加社会实践的老师、家长与学生各有多少人?
(2)由于各种原因,二等座火车票单程只能买x张(x小于参加社会实践的人数),其余的须买一等座火车票,在保证每位参与人员都有座位坐的前提下,请你设计最经济的购票方案,并写出购买火车票的总费用(单程)y与x之间的函数关系式.
| 运行区间 | 公布票价 | 学生票 | ||
| 上车站 | 下车站 | 一等座 | 二等座 | 二等座 |
| 长沙 | 井冈山 | 81(元) | 68(元) | 51(元) |
(2)由于各种原因,二等座火车票单程只能买x张(x小于参加社会实践的人数),其余的须买一等座火车票,在保证每位参与人员都有座位坐的前提下,请你设计最经济的购票方案,并写出购买火车票的总费用(单程)y与x之间的函数关系式.
10.甲仓库有水泥110吨,乙仓库有水泥70吨,现要将这些水泥全部运往A,B两工地,调运任务承包给某运输公司.已知A工地需水泥100吨,B工地需水泥80吨,从甲仓库运往A,B两工地的路程和每吨每千米的运费如表:
(1)设甲仓库运往A地水泥x吨,则甲仓库运往B地水泥110-x吨,乙仓库运往A地水泥100-x吨,乙仓库运往B地水泥x-30吨(用含x的代数式表示);
(2)求总运费W关于x的函数关系式,并求出自变量的取值范围;
(3)当甲、乙两仓库各运往A,B两工地多少吨水泥时,总运费最省?最省的总运费是多少?
| 路程(千米) | 运费(元/吨.千米) | |||
| 甲仓库 | 乙仓库 | 甲仓库 | 乙仓库 | |
| A地 | 25 | 20 | 1 | 0.8 |
| B地 | 20 | 15 | 1.2 | 1.2 |
(2)求总运费W关于x的函数关系式,并求出自变量的取值范围;
(3)当甲、乙两仓库各运往A,B两工地多少吨水泥时,总运费最省?最省的总运费是多少?
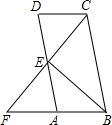 如图,在?ABCD中,BC=2CD,E为AD的中点,CE,BA的延长线交于点F,求证:∠F=∠BCF.
如图,在?ABCD中,BC=2CD,E为AD的中点,CE,BA的延长线交于点F,求证:∠F=∠BCF. 如图,有一条小路穿过长方形的草地ABCD,若AB=60m,BC=84m,AE=100m,AE∥CF,则这条小路AECF的面积是多少?
如图,有一条小路穿过长方形的草地ABCD,若AB=60m,BC=84m,AE=100m,AE∥CF,则这条小路AECF的面积是多少?