题目内容
9.(1)计算:$\sqrt{8}$+($\frac{1}{2}$)-2-4cos45°(2)解方程:$\frac{x}{x+1}$-$\frac{4}{{x}^{2}-1}$=1.
分析 (1)原式利用负整数指数幂法则,二次根式性质,以及特殊角的三角函数值计算即可得到结果;
(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)原式=2$\sqrt{2}$+4-2$\sqrt{2}$=4;
(2)去分母得:x2-x-4=x2-1,
解得:x=-3,
经检验x=-3是方程的根.
点评 此题考查了解分式方程,以及实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
1.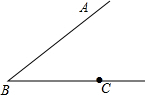 如图,点C是∠ABC一边上一点
如图,点C是∠ABC一边上一点
(1)按下列要求进行尺规作图:
①作线段BC的中垂线DE,E为垂足.
②作∠ABC的平分线BD.
③连结CD,并延长交BA于F.
(2)若∠ABC=62°,求∠BFC的度数.
 如图,点C是∠ABC一边上一点
如图,点C是∠ABC一边上一点(1)按下列要求进行尺规作图:
①作线段BC的中垂线DE,E为垂足.
②作∠ABC的平分线BD.
③连结CD,并延长交BA于F.
(2)若∠ABC=62°,求∠BFC的度数.
19.在平行四边形、菱形、矩形、正方形中,能使一个点到各顶点距离相等的图形是( )
| A. | 菱形和矩形 | B. | 菱形和正方形 | ||
| C. | 矩形和正方形 | D. | 平行四边形和菱形 |
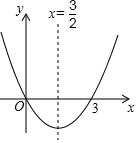 如图所示的二次函数图象上有3个点(-3,y1),(m,y2),(2,y3),若y1>y2>y3,则m可以取得的最大整数值为( )
如图所示的二次函数图象上有3个点(-3,y1),(m,y2),(2,y3),若y1>y2>y3,则m可以取得的最大整数值为( )