题目内容
1.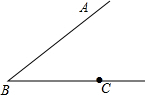 如图,点C是∠ABC一边上一点
如图,点C是∠ABC一边上一点(1)按下列要求进行尺规作图:
①作线段BC的中垂线DE,E为垂足.
②作∠ABC的平分线BD.
③连结CD,并延长交BA于F.
(2)若∠ABC=62°,求∠BFC的度数.
分析 (1)根据线段垂直平分线的画法.角平分线的画法,画出图形即可.
(2)根据∠BFC=180°-∠FBC-∠FCB,求出∠FCB即可.
解答 解:(1)答案如图所示.
(2)∵∠ABC=62°,BD为∠ABC的平分线
∴∠ABD=∠CBD=31°
∵DE是BC的中垂线
∴BD=CD
∴∠CBD=∠DCB=31°
∴∠BFC=180°-∠FBC-∠FCB=180°-62°-31°=87°.
点评 本题考查作图、复杂作图、线段的垂直平分线的性质等知识,解题的关键是熟练掌握基本作图,利用线段垂直平分线上的点到线段的两个端点距离相等,寻找等腰三角形解决问题,属于中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.若等腰三角形中有一个角等于70°,则这个等腰三角形的顶角的度数是( )
| A. | 70° | B. | 40° | C. | 70°或40° | D. | 70°或55° |
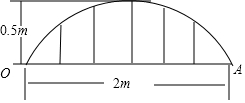 某公司草坪的护栏是由50段形状相同的抛物线组成的,为牢固起见,每段护栏需按间距0.4m 加设不锈钢管(如图)做成立柱.为了计算所需不锈钢管立柱的总长度,设计人员测得如图所示的数据.
某公司草坪的护栏是由50段形状相同的抛物线组成的,为牢固起见,每段护栏需按间距0.4m 加设不锈钢管(如图)做成立柱.为了计算所需不锈钢管立柱的总长度,设计人员测得如图所示的数据. 实数a、b在数轴上的位置如图所示,则化简|a+2b|-|a-b|的结果为2a+b.
实数a、b在数轴上的位置如图所示,则化简|a+2b|-|a-b|的结果为2a+b. 如图,一拱桥呈抛物线状,桥的最大高度是16m,跨度是40m,求在线段AB上离中心M处15m的地方,桥的高度是多少?
如图,一拱桥呈抛物线状,桥的最大高度是16m,跨度是40m,求在线段AB上离中心M处15m的地方,桥的高度是多少? 小刚手里有一根长为80cm的木棒,他把木棒垂直放置在地面上(如图所示),此时测出该木棒在太阳光下的影子的长度为60cm,小刚绕木棒与地面的接触点转动该木棒,想尽办法使木棒的影子最长;问:该木棒转到什么位置时影子最长?并求出此时影子的长度.
小刚手里有一根长为80cm的木棒,他把木棒垂直放置在地面上(如图所示),此时测出该木棒在太阳光下的影子的长度为60cm,小刚绕木棒与地面的接触点转动该木棒,想尽办法使木棒的影子最长;问:该木棒转到什么位置时影子最长?并求出此时影子的长度.