题目内容

7．已知a2+4a+$\sqrt{b+2}$=-4，求|2a+b|-|b-2a|的值．

分析 将已知等式转化为（a+2）2+$\sqrt{b+2}$=0，利用非负数的性质求得a、b的值．然后将其代入所求的代数式进行求值即可．

解答 解：由a2+4a+$\sqrt{b+2}$=-4，得
（a+2）2+$\sqrt{b+2}$=0，
则a+2=0，b+2=0，
所以a=b=-2．
所以|2a+b|-|b-2a|=|3a|-|-a|=|-6|+|2|=6+2=8．

点评 本题考查了配方法的应用，非负数的性质．解题时要注意配方法的步骤．注意在变形的过程中不要改变式子的值．

练习册系列答案
相关题目
17．配方法是一种常用的数学方法，用配方法将6-2$\sqrt{5}$写成平方形式的方法是：6-2$\sqrt{5}$=5+1-2$\sqrt{5}$=（$\sqrt{5}$）2+（$\sqrt{1}$）2-2$\sqrt{5}$=（$\sqrt{5}$-1）2．利用这个方法解决：
（1）5+2$\sqrt{6}$=（$\sqrt{2}$+$\sqrt{3}$）2，5-2$\sqrt{6}$=（$\sqrt{2}$-$\sqrt{3}$）2；
（2）化简$\sqrt{11-2\sqrt{30}}+\sqrt{7-2\sqrt{10}}$；
（3）当1≤x≤2时，化简$\sqrt{x+2\sqrt{x-1}}+\sqrt{x-2\sqrt{x-1}}$．
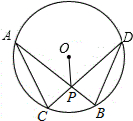18．如图，在⊙O中，弦AB、CD相交于点P，若AB=CD，∠APO=65°，则∠APC=50 度．
15．根据要求，用尺规作图：已知：∠AOB，点P在OA上，过点P作直线HD，使HD∥OB．（不写作法，保留作图痕迹）
2．用反证法证明“三角形的内角中最多有一个角是直角”时应假设：三角形中有两个角是直角．
12．若关于x，y的方程组$\left\{\begin{array}{l}{x-3y=k-2}\\{5x-3y=k}\end{array}\right.$的解x与y相等，那么k的值是1．
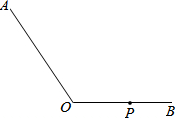19．作图并填空：如图，在∠AOB中，点P在边OB上，
（1）过点P分别作直线OB、直线OA的垂线，交直线OA于点M、N；
（2）点P到直线OA的距离是线段PN的长度；
（3）点O到直线PN的距离是线段ON的长度．
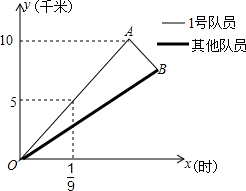16．自行车队点的一次训练中，1号队员以高于其他队员10千米/时的速度独自前行，匀速行进一段时间后，又返回队伍，在往返过程中速度保持不变，设分开后行进的时间为x小时，1号队员和其他队员行进的路程分别为y1、y2（千米），且y1、y2与x的函数关系如图所示．
（1）1号队员返回队伍时距离出发地多远？
（2）在多长时间内，1号队员与其他队员之间的距离大于2千米？
17．在平面直角坐标系中，已知线段AB的两个端点分别是A（-4，-1），B（1，1），将线段AB平移后得到线段A′B′，若点A′的坐标为（-2，3），则点B′的坐标为（　　）
A．（-1，5）B．（3，5）C．（3，-3）D．（-1，-3）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网