题目内容
19.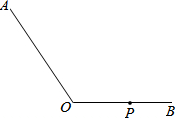 作图并填空:如图,在∠AOB中,点P在边OB上,
作图并填空:如图,在∠AOB中,点P在边OB上,(1)过点P分别作直线OB、直线OA的垂线,交直线OA于点M、N;
(2)点P到直线OA的距离是线段PN的长度;
(3)点O到直线PN的距离是线段ON的长度.
分析 (1)首先利用直尺和三角板做出图形,然后再表上垂足和直角符号;
(2)、(3)根据点到直线的距离的定义解答即可.
解答 解:(1)如图所示:
(2)点P到直线OA的距离是PN线段的长度;
(3)点O到直线PN的距离是线段ON的长度.
点评 本题主要考查的是点到直线的距离,掌握垂线的做法和点到直线的距离的定义是解题的关键.

练习册系列答案
相关题目
14.在平面直角坐标系中,已知O是原点,四边形ABCD是长方形,A,B,C的坐标分别为A(-3,1),B(-3,3),C(2,3).
(1)求D点坐标;
(2)将长方形ABCD以每秒1个单位长度的速度水平向右平移,2秒钟后所得的四边形A1B1C1D1四个顶点的坐标各是多少?
请将(1)(2)中的答案直接填入下表:
(3)平移(2)中长方形ABCD,几秒钟后△OBD的面积等于长方形ABCD的面积.
(1)求D点坐标;
(2)将长方形ABCD以每秒1个单位长度的速度水平向右平移,2秒钟后所得的四边形A1B1C1D1四个顶点的坐标各是多少?
请将(1)(2)中的答案直接填入下表:
| 点 | D | A1 | B1 | C1 | D1 |
| 坐标 |
11.实验学校计划阻值共青团员372人到某爱国主义基地接受教育,并安排8位老师同行,经学校与汽车出租公司协商,有两种型号客车可供选择,它们的载客量和租金如表所示,为了保证每人都有座位,学校决定租8辆车.
(1)写出符合要求的租车方案,并说明理由;
(2)设租甲种客车x辆,总租金共y(元),写出y与x之间的函数关系式;
(3)在(1)的方案中,求出租金最少的租车方案.
(1)写出符合要求的租车方案,并说明理由;
(2)设租甲种客车x辆,总租金共y(元),写出y与x之间的函数关系式;
(3)在(1)的方案中,求出租金最少的租车方案.
| 车种 人数与租金 单位 | 甲种客车 | 乙种客车 |
| 载客量(单位:人/辆) | 50 | 30 |
| 租金(单位:元/辆) | 400 | 200 |
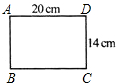 如图,木工师傅要以旧翻新一张桌面,打算把一块长宽为20cm和14cm的矩形桌面ABCD的四个角锯成半径为5cm,并且与两边相切的圆弧形.请你在木板上把其中一个角的圆弧线画出来(要求尺规作图,保留画图痕迹),并求出新桌面面积.
如图,木工师傅要以旧翻新一张桌面,打算把一块长宽为20cm和14cm的矩形桌面ABCD的四个角锯成半径为5cm,并且与两边相切的圆弧形.请你在木板上把其中一个角的圆弧线画出来(要求尺规作图,保留画图痕迹),并求出新桌面面积.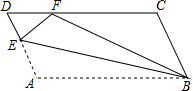 如图,平行四边形ABCD中,点E在AD上,以BE为折痕,把△ABE向上翻折,点A正好落在CD边的点F处.若△FDE的周长为6,平行四边形ABCD的周长为26,那么CF的长为7.
如图,平行四边形ABCD中,点E在AD上,以BE为折痕,把△ABE向上翻折,点A正好落在CD边的点F处.若△FDE的周长为6,平行四边形ABCD的周长为26,那么CF的长为7.