题目内容
18.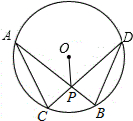 如图,在⊙O中,弦AB、CD相交于点P,若AB=CD,∠APO=65°,则∠APC=50 度.
如图,在⊙O中,弦AB、CD相交于点P,若AB=CD,∠APO=65°,则∠APC=50 度.
分析 连接OA、OD,证明△APC≌△DPB和△AOP≌△DOP,求出∠APD的度数,根据邻补角的性质得到答案.
解答 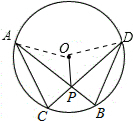 解:连接OA、OD,
解:连接OA、OD,
∵AB=CD,
∴$\widehat{AB}$=$\widehat{CD}$,
∴$\widehat{AC}$=$\widehat{BD}$,
∴AC=BD,
在△APC和△DPB中,
$\left\{\begin{array}{l}{∠PAC=∠PDB}\\{∠APC=∠DPB}\\{AC=BD}\end{array}\right.$,
∴△APC≌△DPB,
∴PA=PD,
在△AOP和△DOP中,
$\left\{\begin{array}{l}{PA=PD}\\{OA=OD}\\{OP=OP}\end{array}\right.$,
∴△AOP≌△DOP,
∴∠APO=∠DPO=65°,
∴∠APD=130°,
∴∠APC=50°.
故答案为:50°.
点评 本题考查的是圆心角、弧、弦的关系和全等三角形的判定和性质,正确作出辅助线、灵活运用相关的性质和判定定理是解题的关键.

练习册系列答案
相关题目
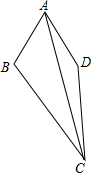 如图,四边形ABCD中,∠BAD=60°,∠BCD=30°,AB=AD,BC=8cm,CD=5cm,则AC的长为$\sqrt{89}$cm.
如图,四边形ABCD中,∠BAD=60°,∠BCD=30°,AB=AD,BC=8cm,CD=5cm,则AC的长为$\sqrt{89}$cm.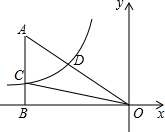 如图,已知双曲线y=$\frac{k}{x}$(k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若△AOC的面积为9,则k的( )
如图,已知双曲线y=$\frac{k}{x}$(k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若△AOC的面积为9,则k的( )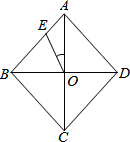 如图,已知菱形ABCD的一个内角∠BAD=80°,对角线AC、BD相交于点O,点E在AB上,且BE=BO,求∠EOA的度数.
如图,已知菱形ABCD的一个内角∠BAD=80°,对角线AC、BD相交于点O,点E在AB上,且BE=BO,求∠EOA的度数.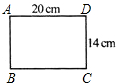 如图,木工师傅要以旧翻新一张桌面,打算把一块长宽为20cm和14cm的矩形桌面ABCD的四个角锯成半径为5cm,并且与两边相切的圆弧形.请你在木板上把其中一个角的圆弧线画出来(要求尺规作图,保留画图痕迹),并求出新桌面面积.
如图,木工师傅要以旧翻新一张桌面,打算把一块长宽为20cm和14cm的矩形桌面ABCD的四个角锯成半径为5cm,并且与两边相切的圆弧形.请你在木板上把其中一个角的圆弧线画出来(要求尺规作图,保留画图痕迹),并求出新桌面面积.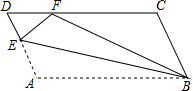 如图,平行四边形ABCD中,点E在AD上,以BE为折痕,把△ABE向上翻折,点A正好落在CD边的点F处.若△FDE的周长为6,平行四边形ABCD的周长为26,那么CF的长为7.
如图,平行四边形ABCD中,点E在AD上,以BE为折痕,把△ABE向上翻折,点A正好落在CD边的点F处.若△FDE的周长为6,平行四边形ABCD的周长为26,那么CF的长为7.