题目内容
16.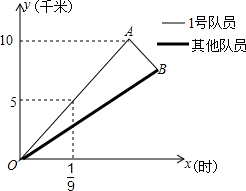 自行车队点的一次训练中,1号队员以高于其他队员10千米/时的速度独自前行,匀速行进一段时间后,又返回队伍,在往返过程中速度保持不变,设分开后行进的时间为x小时,1号队员和其他队员行进的路程分别为y1、y2(千米),且y1、y2与x的函数关系如图所示.
自行车队点的一次训练中,1号队员以高于其他队员10千米/时的速度独自前行,匀速行进一段时间后,又返回队伍,在往返过程中速度保持不变,设分开后行进的时间为x小时,1号队员和其他队员行进的路程分别为y1、y2(千米),且y1、y2与x的函数关系如图所示.(1)1号队员返回队伍时距离出发地多远?
(2)在多长时间内,1号队员与其他队员之间的距离大于2千米?
分析 (1)根据待定系数法,可得OA函数解析式,根据函数值,可得相应的自变量求出点A的坐标,根据1号队员以高于其他队员10千米/时的速度独自前行,所以其他队员的速度为45-10=35(千米/时),得到OB的函数关系式为y=35x,设点B的坐标为(x,35x),根据在往返过程中速度保持不变,得到方程$\frac{10-35x}{x-\frac{2}{9}}=45$,解得:x=$\frac{1}{4}$,点B的坐标为($\frac{1}{4}$,$\frac{35}{4}$),即可解答;
(2)分类讨论,根据行进时,距离大于2,返回时距离大于2,可得一元一次不等式组,根据解不等式组,可得答案.
解答 解:(1)设OA的函数关系式为y=kx,
把($\frac{1}{9}$,5)代入得,5=$\frac{1}{9}$k,
解得:k=45,
∴y=45x,
即1号队员的速度为45千米/时,
当y=10时,10=45x,
解得:x=$\frac{2}{9}$,
∴点A的坐标为($\frac{2}{9}$,10)
∵1号队员以高于其他队员10千米/时的速度独自前行,
∴其他队员的速度为45-10=35(千米/时),
∴OB的函数关系式为y=35x,
设点B的坐标为(x,35x),
∵在往返过程中速度保持不变,
∴$\frac{10-35x}{x-\frac{2}{9}}=45$,
解得:x=$\frac{1}{4}$,
35x=$\frac{35}{4}$,
∴点B的坐标为($\frac{1}{4}$,$\frac{35}{4}$),
∴1号队员返回队伍时距离出发地$\frac{35}{4}$千米.
(2)设x小时时,1号队员与其他队员之间的距离大于2千米,根据题意,得
$\left\{\begin{array}{l}{45x-35x>2}\\{20-45x-35x>2}\end{array}\right.$,
解得:$\frac{1}{5}$<x<$\frac{9}{40}$.
答:在$\frac{1}{5}$<x<$\frac{9}{40}$时,1号队员与其他队员之间的距离大于2千米.
点评 本题考查了一次函数的应用,利用了函数与自变量的关系,一元一次方程的应用,一元一次不等式组的应用,题目稍有难度.

 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案(1)写出符合要求的租车方案,并说明理由;
(2)设租甲种客车x辆,总租金共y(元),写出y与x之间的函数关系式;
(3)在(1)的方案中,求出租金最少的租车方案.
| 车种 人数与租金 单位 | 甲种客车 | 乙种客车 |
| 载客量(单位:人/辆) | 50 | 30 |
| 租金(单位:元/辆) | 400 | 200 |
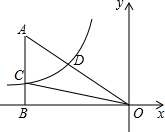 如图,已知双曲线y=$\frac{k}{x}$(k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若△AOC的面积为9,则k的( )
如图,已知双曲线y=$\frac{k}{x}$(k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若△AOC的面积为9,则k的( )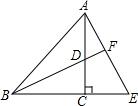 如图,在△ABC中,∠ACB=90°,D为AC上一点,延长BC到点E,使CE=CD,连接AE且与BD的延长线交于点F,若AE=BD,求证:BD⊥AE.
如图,在△ABC中,∠ACB=90°,D为AC上一点,延长BC到点E,使CE=CD,连接AE且与BD的延长线交于点F,若AE=BD,求证:BD⊥AE.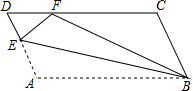 如图,平行四边形ABCD中,点E在AD上,以BE为折痕,把△ABE向上翻折,点A正好落在CD边的点F处.若△FDE的周长为6,平行四边形ABCD的周长为26,那么CF的长为7.
如图,平行四边形ABCD中,点E在AD上,以BE为折痕,把△ABE向上翻折,点A正好落在CD边的点F处.若△FDE的周长为6,平行四边形ABCD的周长为26,那么CF的长为7.