题目内容
(1)解方程:x2+2x-4﹦0;
(2)解不等式组
,并写出不等式组的整数解.
(2)解不等式组
|
考点:解一元二次方程-配方法,解一元一次不等式组,一元一次不等式组的整数解
专题:
分析:(1)把常数项-4移项后,应该在左右两边同时加上一次项系数2的一半的平方.
(2)先解出不等式组的解集,再找出x取值范围的整数解.
(2)先解出不等式组的解集,再找出x取值范围的整数解.
解答:解:(1)把方程x2+2x-4=0的常数项移到等号的右边,得
x2+2x=4,
方程两边同时加上一次项系数一半的平方,得
x2+2x+1=4+1,
配方,得
(x+1)2=5,
直接开平方,得
x+1=±
,
解得x1=-1+
,x2=-1-
;
(2)
整理2x+5≤3(x+2)得,
x≥-1,
整理
<
得,
x<3,
故解不等式组可得解集为-1≤x<3,
∴不等式组的整数解:-1,0,1,2.
x2+2x=4,
方程两边同时加上一次项系数一半的平方,得
x2+2x+1=4+1,
配方,得
(x+1)2=5,
直接开平方,得
x+1=±
| 5 |
解得x1=-1+
| 5 |
| 5 |
(2)
|
整理2x+5≤3(x+2)得,
x≥-1,
整理
| x-1 |
| 2 |
| x |
| 3 |
x<3,
故解不等式组可得解集为-1≤x<3,
∴不等式组的整数解:-1,0,1,2.
点评:(1)主要考查了配方法的一般步骤:
①把常数项移到等号的右边;
②把二次项的系数化为1;
③等式两边同时加上一次项系数一半的平方.
选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.
(2)主要考查了解不等式组,关键是正确解出不等式的解集.
①把常数项移到等号的右边;
②把二次项的系数化为1;
③等式两边同时加上一次项系数一半的平方.
选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.
(2)主要考查了解不等式组,关键是正确解出不等式的解集.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 请把下面证明过程补充完整:
请把下面证明过程补充完整: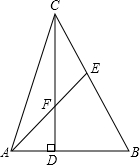 已知:如图,在△ABC中,CD⊥AB于点D,AD=2,BD=3,CD=6,点E是BC上一点,
已知:如图,在△ABC中,CD⊥AB于点D,AD=2,BD=3,CD=6,点E是BC上一点,
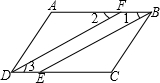
 如图,在等腰梯形ABCD中,AD∥BC,AB=AD=DC,∠B=60°,NC=
如图,在等腰梯形ABCD中,AD∥BC,AB=AD=DC,∠B=60°,NC=