题目内容
（x2+xy+y2）（x2+xy+2y2）-12y4．
考点：因式分解
专题：
分析：将x2+xy+y2看作整体，进而利用十字相乘法分解因式得出即可．
解答：解：原式=（x2+xy+y2）（x2+xy+y2+y2）-12y4
=（x2+xy+y2）2+y2（x2+xy+y2）-12y4
=（x2+xy+y2+4y2）（x2+xy+y2-3y2）
=（x2+xy+5y2）（x2+xy-2y2）
=（x2+xy+5y2）（x+2y）（x-y）．
=（x2+xy+y2）2+y2（x2+xy+y2）-12y4
=（x2+xy+y2+4y2）（x2+xy+y2-3y2）
=（x2+xy+5y2）（x2+xy-2y2）
=（x2+xy+5y2）（x+2y）（x-y）．
点评：此题主要考查了因式分解法的应用，熟练利用十字相乘法分解因式是解题关键．
练习册系列答案
相关题目
如图，已知?ABCD，E，F是对角线BD上的两点，且BE=DF．
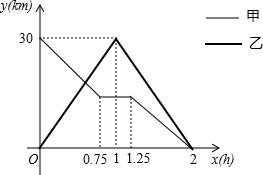在一条笔直的公路上有A、B两地．甲、乙两人同时出发，甲骑电动车从A地到B地，中途出现故障后停车维修，修好车后以原速继续行驶到B地；乙骑摩托车从B地到A地，到达A地后立即按原路原速返回，结果两人同时到B地．如图是甲、乙两人与B地的距离y（km）与乙行驶时间x（h）之间的函数图象．
如图，在梯形ABCD中，AD∥BC，∠D=90°，BE⊥AC，E为垂足，AC=BC．