题目内容
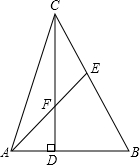 已知:如图,在△ABC中,CD⊥AB于点D,AD=2,BD=3,CD=6,点E是BC上一点,
已知:如图,在△ABC中,CD⊥AB于点D,AD=2,BD=3,CD=6,点E是BC上一点,| CE |
| BE |
| 4 |
| 5 |
(1)求BE的长;
(2)求证:∠BAE=∠BCA;
(3)求证:tan∠CFE=1.
考点:勾股定理,相似三角形的判定与性质
专题:
分析:(1)运用勾股定理求出BC的长,再用BC乘BE占BC的分数求解.
(2)利用△ABE∽△CBA,求出∠BAE=∠BCA.
(3)作BM⊥AC于点M,求出BM=CM,再求出∠CFE=45°,得出tan∠CFE=1.
(2)利用△ABE∽△CBA,求出∠BAE=∠BCA.
(3)作BM⊥AC于点M,求出BM=CM,再求出∠CFE=45°,得出tan∠CFE=1.
解答:解:(1)∵CD⊥AB于点D,BD=3,CD=6,
∴BC=
=3
,
∵
=
,
∴BE=
BC=
×3
=
.
(2)证明:∵AB=5,BE=
,BC=3
,
∴
=5÷
=
,
=3
÷5=
,
∴
=
∴△ABE∽△CBA,
∴∠BAE=∠BCA.
(3)证明:作BM⊥AC于点M,
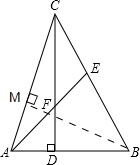
∵CD⊥AB于点D,AD=2,CD=6,
∴AC=
=2
,
∵
AB•CD=
AC•BM,
∴BM=
=
=
,
∴CM=
=
=
=BM,
∴∠BCA=45°,
∴∠BAE=45°,
∴∠AFD=45°,
∴∠CFE=45°,
∴tan∠CFE=1.
∴BC=
| 62+32 |
| 5 |
∵
| CE |
| BE |
| 4 |
| 5 |
∴BE=
| 5 |
| 9 |
| 5 |
| 9 |
| 5 |
5
| ||
| 3 |
(2)证明:∵AB=5,BE=
5
| ||
| 3 |
| 5 |
∴
| AB |
| BE |
5
| ||
| 3 |
3
| ||
| 5 |
| BC |
| AB |
| 5 |
3
| ||
| 5 |
∴
| AB |
| BE |
| BC |
| AB |
∴△ABE∽△CBA,
∴∠BAE=∠BCA.
(3)证明:作BM⊥AC于点M,

∵CD⊥AB于点D,AD=2,CD=6,
∴AC=
| 62+22 |
| 10 |
∵
| 1 |
| 2 |
| 1 |
| 2 |
∴BM=
| AB?CD |
| AC |
| 5•6 | ||
2
|
3
| ||
| 2 |
∴CM=
| BC2-BM2 |
45-
|
3
| ||
| 2 |
∴∠BCA=45°,
∴∠BAE=45°,
∴∠AFD=45°,
∴∠CFE=45°,
∴tan∠CFE=1.
点评:本题主要考查勾股定理,三角形相似的知识,关键是找准直角三角形灵活运用勾股定理.

练习册系列答案
相关题目
下列图形中,既是轴对称图形又是中心对称图形的是( )
A、 |
B、 |
C、 |
D、 |
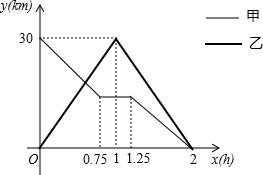 在一条笔直的公路上有A、B两地.甲、乙两人同时出发,甲骑电动车从A地到B地,中途出现故障后停车维修,修好车后以原速继续行驶到B地;乙骑摩托车从B地到A地,到达A地后立即按原路原速返回,结果两人同时到B地.如图是甲、乙两人与B地的距离y(km)与乙行驶时间x(h)之间的函数图象.
在一条笔直的公路上有A、B两地.甲、乙两人同时出发,甲骑电动车从A地到B地,中途出现故障后停车维修,修好车后以原速继续行驶到B地;乙骑摩托车从B地到A地,到达A地后立即按原路原速返回,结果两人同时到B地.如图是甲、乙两人与B地的距离y(km)与乙行驶时间x(h)之间的函数图象.
 如图,在平面直角坐标系xOy中,已知抛物线y=-x(x-3)(0≤x≤3)在x轴上方的部分,记作C1,它与x轴交于点O,A1,将C1绕点A1旋转180°得C2,C2与x 轴交于另一点A2.请继续操作并探究:将C2绕点A2旋转180°得C3,与x轴交于另一点A3;将C3绕点A2旋转180°得C4,与x轴交于另一点A4,这样依次得到x轴上的点A1,A2,A3,…,An,…,及抛物线C1,C2,…,Cn,….则点A4的坐标为
如图,在平面直角坐标系xOy中,已知抛物线y=-x(x-3)(0≤x≤3)在x轴上方的部分,记作C1,它与x轴交于点O,A1,将C1绕点A1旋转180°得C2,C2与x 轴交于另一点A2.请继续操作并探究:将C2绕点A2旋转180°得C3,与x轴交于另一点A3;将C3绕点A2旋转180°得C4,与x轴交于另一点A4,这样依次得到x轴上的点A1,A2,A3,…,An,…,及抛物线C1,C2,…,Cn,….则点A4的坐标为