题目内容
4.阅读探索:(1)若a>b,b>c,则a,c的大小关系是a>c.若a≥b,b≥c,则a,c的大小关系是a≥c.若a≥b,b>c,则a,c的大小关系是a>c.
拓展提高:
(2)已知a>b,m>n,试比较a+m与b+n的大小,并结合上述规律说明理由.
能力运用:
(3)已知x,y满足-2≤x+y≤4,0≤2x-y<8,分别求出x,y的取值范围.
分析 (1)利用不等式的性质,直接填空即可;
(2)利用(1)的方法,得出答案即可;
(3)利用(1)的方法,两个不等式对应相加得出x的取值范围,把不等式①乘-2再与不等式②相加,整理得出y的取值范围即可.
解答 解:(1)若a>b,b>c,则a,c的大小关系是a>c.若a≥b,b≥c,则a,c的大小关系是a≥c.若a≥b,b>c,则a,c的大小关系是a>c.
(2)a+m>b+n.
理由:∵a>b,m>n,
∴a+m>b+m>b+n;
(3)①-2≤x+y≤4,
②0≤2x-y<8,
①+②得-2≤3x<12,
-$\frac{2}{3}$≤x<4;
∵-8≤-2x-2y≤4,0≤2x-y<8,
∴-8≤-3y<12,
∴-4<y≤$\frac{8}{3}$
点评 此题考查不等式的性质,掌握不等式的传递性是解决问题的关键.

练习册系列答案
相关题目
 如图所示,OA、OB是两条相交的高速公路,C、D是两处村庄,某百货集团响应新农村建设的要求,要在高速路内建一座大型便民超市P,使PC=PD,且P到∠AOB的两边OA、OB的距离相等,那么超市P的位置应选在哪里?
如图所示,OA、OB是两条相交的高速公路,C、D是两处村庄,某百货集团响应新农村建设的要求,要在高速路内建一座大型便民超市P,使PC=PD,且P到∠AOB的两边OA、OB的距离相等,那么超市P的位置应选在哪里?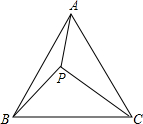 数学探究课上老师处这样一道题:“如图,等边△ABC中有一点P,且PA=3,PB=4,PC=5,试求∠APB的度数.”小明和小军探讨时发现了一种求∠APB度数的方法,下面是这种方法的一部分思路,请按照下列思路要求画图或判断
数学探究课上老师处这样一道题:“如图,等边△ABC中有一点P,且PA=3,PB=4,PC=5,试求∠APB的度数.”小明和小军探讨时发现了一种求∠APB度数的方法,下面是这种方法的一部分思路,请按照下列思路要求画图或判断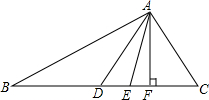 如图,AD、AE、AF分别是△ABC的中线、角平分线和高,请你指出图中相等的角及相等的线段.
如图,AD、AE、AF分别是△ABC的中线、角平分线和高,请你指出图中相等的角及相等的线段.