题目内容
12.在矩形ABCD中,对角线AC,BD相交于点O,CH⊥BD于点H,若∠BCH=28°,则∠OCH的度数为34°.分析 由矩形的性质得出OC=$\frac{1}{2}$AC,OB=$\frac{1}{2}$BD,AC=BD,得出OB=OC,得出∠OBC=∠OCB,求出∠OBC=∠OCB=62°,即可得出∠OCH的度数.
解答 解:如图所示:
∵四边形ABCD是矩形,
∴OC=$\frac{1}{2}$AC,OB=$\frac{1}{2}$BD,AC=BD,
∴OB=OC,
∴∠OBC=∠OCB,
∵CH⊥BD,
∴∠CHB=90°,
∴∠OBC=90°-28°=62°,
∴∠OCB=62°,
∴∠OCH=∠OCB-∠BCH=62°-28°=34°.
点评 本题考查了矩形的性质、等腰三角形的性质、角的互余关系;熟练掌握矩形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
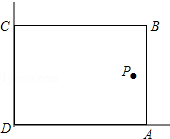 在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=x(m).
在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=x(m).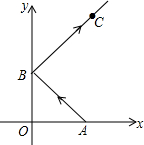 如图,从点A(2,0)发出的一束光,经y轴反射,过点C(3,5),则B点的坐标为(0,2).
如图,从点A(2,0)发出的一束光,经y轴反射,过点C(3,5),则B点的坐标为(0,2). 如图,⊙O的弦ED,CB的延长线交于点A,若BD⊥AE,AB=4,BC=2,AD=3,则DE=5,CD=3$\sqrt{2}$.
如图,⊙O的弦ED,CB的延长线交于点A,若BD⊥AE,AB=4,BC=2,AD=3,则DE=5,CD=3$\sqrt{2}$. 如图,△ABC中,D、E分别是AB、AC的中点.求证:DE=$\frac{1}{2}$BC,DE∥BC.
如图,△ABC中,D、E分别是AB、AC的中点.求证:DE=$\frac{1}{2}$BC,DE∥BC.