题目内容
16.某商场以每件42元的价格购进一种服装,由试销知,每天的销量t与每件的销售价x(元)之间的函数关系为t=204-3x.(1)试写出每天销售这种服装的毛利润y(元)与每件销售价x(元)之间的函数表达式(毛利润=销售价-进货价); 并求出自变量的取值范围.
(2)每件销售价为多少元,才能使每天的毛利润最大?最大毛利润是多少?
分析 (1)根据毛利润=销售价-进货价可得y关于x的函数解析式;
(2)将(1)中函数关系式配方可得最值情况.
解答 解:(1)根据题意,y=(x-42)t=(x-42)(-3x+204)=-3x2+330x-8568,
由$\left\{\begin{array}{l}{x≥42}\\{204-3x≥0}\end{array}\right.$得42≤x≤68;
(2)∵y=-3x2+330x-8568=-3(x-55)2+507,
∴当x=55时,y的最大值507元;
点评 本题主要考查二次函数的应用,理解题意根据相等关系列出函数关系式,并熟练掌握二次函数的性质是解题的关键.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
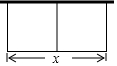 如图,要建一个长方形养鸡场,鸡场的一边靠墙(墙足够长),如果用50m长的篱笆围成中间有一道篱笆墙的养鸡场,设它的长度为x(篱笆墙的厚度忽略不计).
如图,要建一个长方形养鸡场,鸡场的一边靠墙(墙足够长),如果用50m长的篱笆围成中间有一道篱笆墙的养鸡场,设它的长度为x(篱笆墙的厚度忽略不计). 如图,AB是⊙O的直径,AC是弦,弦AE平分∠BAC,ED⊥AC,交AC的延长线于点D.
如图,AB是⊙O的直径,AC是弦,弦AE平分∠BAC,ED⊥AC,交AC的延长线于点D.