Question

1．如图，AB是⊙O的直径，AC是弦，弦AE平分∠BAC，ED⊥AC，交AC的延长线于点D．
（1）求证：DE是⊙O的切线；
（2）若AB=10，AC=6，求DE的长．

Answer 1

分析 （1）首先连接OE，由弦AE平分∠BAC，易证得OE∥AC，又由ED⊥AC，即可证得OE⊥ED，继而证得结论；
（2）首先过点O作OF⊥AC于点F，易得四边形OEFD是矩形，即可得DE=OF，然后由垂径定理求得OF的长，即可求得答案．

解答 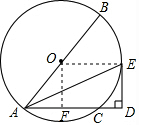（1）证明：连接OE，
∵OA=OE，
∴∠BAE=∠OEA，
∵弦AE平分∠BAC，
∴∠BAE=∠DAE，
∴∠DAE=∠OEA，
∴OE∥AC，
∵ED⊥AC，
∴OE⊥ED，
∴DE是⊙O的切线；

（2）解：过点O作OF⊥AC于点F，
∵ED⊥AC，
∴OF∥ED，AF=$\frac{1}{2}$AC=$\frac{1}{2}$×6=3，
∵OE∥AC，
∴四边形OEFD是矩形，
∴OF=DE，
∵OA=$\frac{1}{2}$AB=$\frac{1}{2}$×10=5，
∴OF=$\sqrt{O{A}^{2}-A{F}^{2}}$=4，
∴DE=OF=4．

点评 此题考查了切线的性质与判定、矩形的判定与性质以及垂径定理．注意准确作出辅助线是解此题的关键．