题目内容
16. 如图,在Rt△ABC中,∠C为直角,CD⊥AB于D,已知AC=3,AB=5,则tan∠BCD等于( )
如图,在Rt△ABC中,∠C为直角,CD⊥AB于D,已知AC=3,AB=5,则tan∠BCD等于( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
分析 根据同角的余角相等得到∠BCD=∠A,根据勾股定理求出BC,根据正切的定义求出tanA,等量代换即可.
解答 解:∵∠C为直角,CD⊥AB,
∴∠A+∠B=90°,∠BCD+∠B=90°,
∴∠BCD=∠A,
∵∠C为直角,AC=3,AB=5,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=4,
∴tanA=$\frac{4}{3}$,
∴tan∠BCD=$\frac{4}{3}$,
故选:B.
点评 本题考查的是锐角三角函数的定义,掌握锐角A的正弦、余弦、正切分别是哪两条边的比是解题的关键.

练习册系列答案
相关题目
11.下列说法正确的是( )
| A. | 每个命题都有逆命题 | B. | 每个定理都有逆定理 | ||
| C. | 所有命题都是定理 | D. | 假命题的逆命题都是假命题 |
1.已知Rt△ABC的直角边AC=BC=4cm,若以C为圆心,以3cm为半径作圆,则这个圆与斜边AB所在直线的位置关系是( )
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 不能确定 |
6.下列四组数中,不是勾股数的一组数是( )
| A. | a=8,b=15,c=17 | B. | a=9,b=12,c=15 | C. | a=7,b=24,c=25 | D. | a=3,b=5,c=7 |
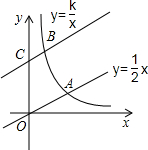 如图,直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点A,将直线y=$\frac{1}{2}$x向上平移3个单位长度后,与y轴交于点C,与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点B,若OA=3BC,则k的值为$\frac{81}{32}$.
如图,直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点A,将直线y=$\frac{1}{2}$x向上平移3个单位长度后,与y轴交于点C,与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点B,若OA=3BC,则k的值为$\frac{81}{32}$.