题目内容
4.已知一次函数y=k(x+5)和反比例函数y=$\frac{6}{x}$的图象都经过点P(3,m).(1)求k的值以及两函数图象交点的坐标.
(2)平行于x轴的直线y=a(a≠0)与这个一次函数的图象相交于点A,与这个反比例函数的图象相交于点B,且PA=PB.求a的值.
分析 (1)利用待定系数法求出点P坐标以及一次函数解析式,解方程组求交点坐标.
(2)用a表示点A、B坐标,作PD⊥AB于D,则D(3,a),分两种情形①当a>0时,②当a<0时讨论即可.
解答 解:(1)把P(m,3)代入y=$\frac{6}{x}$得m=2,则P的坐标是(3,2).
把(3,2)代入y=k(x+5)得k=$\frac{1}{4}$,
则一次函数的解析式是y=$\frac{1}{4}$(x+5).
解方程组$\left\{\begin{array}{l}{y=\frac{1}{4}(x+5)}\\{y=\frac{6}{x}}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$或$\left\{\begin{array}{l}{x=-8}\\{y=-\frac{3}{4}}\end{array}\right.$.
则两个函数的交点坐标是P(3,2)和Q(-8,-$\frac{3}{4}$);
(2)∵行于x轴的直线y=a(a≠0)与这个一次函数的图象相交于点A,与这个反比例函数的图象相交于点B,
∴A(4a-5,a),B($\frac{6}{a}$,a),
作PD⊥AB于D,则D(3,a),
①当a>0时,∵PA=PB,
∴DA=DB,
∴4a-5+$\frac{6}{a}$=6,
∴a=2或$\frac{3}{4}$,
②当a<0时,A、B重合于点Q,即a=-$\frac{3}{4}$也满足条件,
综上所述,a=2或±$\frac{3}{4}$.
点评 本题考查一次函数与反比例函数图象的交点问题、等腰三角形的性质,中点坐标公式等知识,解题的关键是熟练掌握待定系数法,学会利用中点坐标公式,构建方程解决问题,属于中考常考题型.

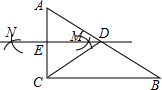 如图,在△ABC中,∠ACB=90°,分别以点A和点C为圆心,以相同的长(大于$\frac{1}{2}$AC)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交AC于点E,连接CD.下列结论错误的是( )
如图,在△ABC中,∠ACB=90°,分别以点A和点C为圆心,以相同的长(大于$\frac{1}{2}$AC)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交AC于点E,连接CD.下列结论错误的是( )| A. | AD=CD | B. | ∠A=∠DCE | C. | ∠ADE=∠DCB | D. | ∠A=2∠DCB |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | a2-b2 | B. | a-b | C. | a+b | D. | a2+b2 |
| A. | 1m | B. | 1.6m | C. | 1.8m | D. | 3m |
 如图,在Rt△ABC中,∠C为直角,CD⊥AB于D,已知AC=3,AB=5,则tan∠BCD等于( )
如图,在Rt△ABC中,∠C为直角,CD⊥AB于D,已知AC=3,AB=5,则tan∠BCD等于( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
