题目内容
20．一位同学在钻研数学题时发现2+1=3，
2×3+1=7，
2×3×5+1=31，
2×3×5×7+1=211．
于是，他根据上面的结果并利用质数表得出结论：从质数2开始，排在前面的任意多个质数的乘积加1一定也是质数．他的结论正确吗？
分析 根据只有1和它本身，再没有别的约数的数是质数；根据除了1和它本身之外还有别的约数的数是合数，可得答案．
解答 解：不正确．
∵2×3×5×7×11×13+1=30031，
30031=59×509，
∴30031是合数，故他的结论不正确．
点评 本题考查了质数与合数，掌握质数与合数的定义是关键．
练习册系列答案
文敬图书课时先锋系列答案
相关题目
15．
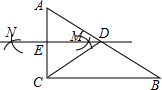如图，在△ABC中，∠ACB=90°，分别以点A和点C为圆心，以相同的长（大于$\frac{1}{2}$AC）为半径作弧，两弧相交于点M和点N，作直线MN交AB于点D，交AC于点E，连接CD．下列结论错误的是（ ）
如图，在△ABC中，∠ACB=90°，分别以点A和点C为圆心，以相同的长（大于$\frac{1}{2}$AC）为半径作弧，两弧相交于点M和点N，作直线MN交AB于点D，交AC于点E，连接CD．下列结论错误的是（ ）| A． | AD=CD | B． | ∠A=∠DCE | C． | ∠ADE=∠DCB | D． | ∠A=2∠DCB |
16．
如图，在Rt△ABC中，∠C为直角，CD⊥AB于D，已知AC=3，AB=5，则tan∠BCD等于（ ）
如图，在Rt△ABC中，∠C为直角，CD⊥AB于D，已知AC=3，AB=5，则tan∠BCD等于（ ）| A． | $\frac{3}{4}$ | B． | $\frac{4}{3}$ | C． | $\frac{3}{5}$ | D． | $\frac{4}{5}$ |