题目内容
7.若$\sqrt{x}$=$\sqrt{a}$-$\frac{2}{\sqrt{a}}$(a>0),则$\frac{x+4+\sqrt{{x}^{2}+8x}}{x+4-\sqrt{{x}^{2}+8x}}$=$\frac{{a}^{2}}{4}$.分析 根据二次根式值分非负性可得a的范围,将已知等式两边平方可得x+4=a+$\frac{4}{a}$,将其代入原式,通过变形即可得其值.
解答 解:∵$\sqrt{x}$=$\sqrt{a}$-$\frac{2}{\sqrt{a}}$,
∴$\sqrt{a}$-$\frac{2}{\sqrt{a}}$≥0,
解得:a≥2,
将$\sqrt{x}$=$\sqrt{a}$-$\frac{2}{\sqrt{a}}$两边平方可得,x=a-4+$\frac{4}{a}$,
∴x+4=a+$\frac{4}{a}$,
∴原式=$\frac{a+\frac{4}{a}+\sqrt{(x+4)^{2}-16}}{a+\frac{4}{a}-\sqrt{(x+4)^{2}-16}}$
=$\frac{a+\frac{4}{a}+\sqrt{(a+\frac{4}{a})^{2}-16}}{a+\frac{4}{a}-\sqrt{(a+\frac{4}{a})^{2}-16}}$
=$\frac{a+\frac{4}{a}+\sqrt{(a-\frac{4}{a})^{2}}}{a+\frac{4}{a}-\sqrt{(a-\frac{4}{a})^{2}}}$
=$\frac{a+\frac{4}{a}+a-\frac{4}{a}}{a+\frac{4}{a}-a+\frac{4}{a}}$
=$\frac{2a}{\frac{8}{a}}$
=$\frac{{a}^{2}}{4}$,
故答案为:$\frac{{a}^{2}}{4}$.
点评 本题主要考查二次根式的化简与求值,熟练掌握二次根式的性质及运算法则是解题的关键.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
15.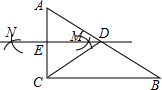 如图,在△ABC中,∠ACB=90°,分别以点A和点C为圆心,以相同的长(大于$\frac{1}{2}$AC)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交AC于点E,连接CD.下列结论错误的是( )
如图,在△ABC中,∠ACB=90°,分别以点A和点C为圆心,以相同的长(大于$\frac{1}{2}$AC)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交AC于点E,连接CD.下列结论错误的是( )
 如图,在△ABC中,∠ACB=90°,分别以点A和点C为圆心,以相同的长(大于$\frac{1}{2}$AC)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交AC于点E,连接CD.下列结论错误的是( )
如图,在△ABC中,∠ACB=90°,分别以点A和点C为圆心,以相同的长(大于$\frac{1}{2}$AC)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交AC于点E,连接CD.下列结论错误的是( )| A. | AD=CD | B. | ∠A=∠DCE | C. | ∠ADE=∠DCB | D. | ∠A=2∠DCB |
12.有下列函数:①y=2x;②y=-x-100;③y=2-3x;④y=x2-1.其中是一次函数的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
19.a4-b4和a2+b2的公因式是( )
| A. | a2-b2 | B. | a-b | C. | a+b | D. | a2+b2 |
16. 如图,在Rt△ABC中,∠C为直角,CD⊥AB于D,已知AC=3,AB=5,则tan∠BCD等于( )
如图,在Rt△ABC中,∠C为直角,CD⊥AB于D,已知AC=3,AB=5,则tan∠BCD等于( )
 如图,在Rt△ABC中,∠C为直角,CD⊥AB于D,已知AC=3,AB=5,则tan∠BCD等于( )
如图,在Rt△ABC中,∠C为直角,CD⊥AB于D,已知AC=3,AB=5,则tan∠BCD等于( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
