题目内容
9.如图,已知抛物线y=ax2+bx+c与x轴交于A(-1,0),B(3,0)两点,与y轴交于C(0,3),DE所在的直线是该抛物线的对称轴.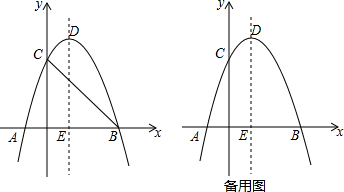
(1)求抛物线的解析式及顶点D的坐标;
(2)连接AD,P是AD上的动点,P′是点P关于DE的对称点,连接PE,过点P′作PF∥PE,交x轴于点F,设四边形PP′FE的面积为y,EF=x,求y与x之间的函数关系式.
分析 (1)只需运用待定系数法就可求出抛物线的解析式,然后运用配方法就可求出顶点D的坐标;
(2)易证四边形PP′FE是平行四边形,要求y与x之间的函数关系式,只需求出EF边上的高(即点P的纵坐标),直线AD的解析式可求,由于P是AD上的动点,只需求出点P的横坐标,只需利用PH=$\frac{1}{2}$PP′=$\frac{1}{2}$EF=$\frac{1}{2}$x就可解决问题.
解答 解:(1)由题可得:
$\left\{\begin{array}{l}{a-b+c=0}\\{9a+3b+c=0}\\{c=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-1}\\{b=2}\\{c=3}\end{array}\right.$,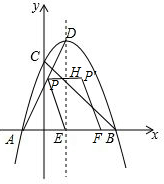
∴抛物线的解析式为y=-x2+2x+3.
由y=-x2+2x+3=-(x-1)2+4,得
顶点D的坐标为(1,4);
(2)设直线AD的解析式为y=mx+n,
把A(-1,0),D(1,4)代入y=mx+n,得
$\left\{\begin{array}{l}{-k+b=0}\\{k+b=4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=2}\\{b=2}\end{array}\right.$,
∴直线AD的解析式为y=2x+2.
∵P′是点P关于DE的对称点,
∴PH=P′H,PP′⊥DE.
∵EF⊥DE,∴PP′∥EF.
又∵P′F∥PE,
∴四边形PP′FE是平行四边形,
∴PP′=EF=x,
∴PH=P′H=$\frac{1}{2}$PP′=$\frac{1}{2}$x,
∴PH=xH-xP=1-xP=$\frac{1}{2}$x,
∴xP=1-$\frac{1}{2}$x.
∵P是AD上的动点,
∴yP=2(1-$\frac{1}{2}$x)+2=4-x,
∴y=EF•EH=x(4-x)=4x-x2=-x2+4x,
∴y与x之间的函数关系式为y=-x2+4x.
点评 本题主要考查了运用待定系数法求抛物线及直线的解析式、平行四边形的判定与性质、轴对称的性质等知识,用x的代数式表示点P的坐标是解决第2小题的关键.

 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案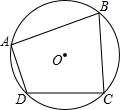 如图,四边形ABCD是⊙O的内接四边形,若∠B=75°,∠C=85°,则∠D-∠A的度数差为( )
如图,四边形ABCD是⊙O的内接四边形,若∠B=75°,∠C=85°,则∠D-∠A的度数差为( )| A. | 10° | B. | 15° | C. | 20° | D. | 25° |
 已知直线y=$\sqrt{3}$x+4$\sqrt{3}$与x轴、y轴分别交于A、B两点,∠ABC=60°,BC与x轴交于C.
已知直线y=$\sqrt{3}$x+4$\sqrt{3}$与x轴、y轴分别交于A、B两点,∠ABC=60°,BC与x轴交于C. MF⊥NF于F,MF交AB于点E,NF交CD于点G,∠1=140°,∠2=50°,试判断AB和CD的位置关系,并说明理由.
MF⊥NF于F,MF交AB于点E,NF交CD于点G,∠1=140°,∠2=50°,试判断AB和CD的位置关系,并说明理由. 如图,直线y=-$\frac{1}{2}$x+4与坐标轴交于A,B两点,C(2,-4),S△PAB=S△ABC,点P在x轴上,求点P的坐标.
如图,直线y=-$\frac{1}{2}$x+4与坐标轴交于A,B两点,C(2,-4),S△PAB=S△ABC,点P在x轴上,求点P的坐标.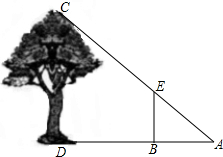 如图,某人在点A处测量树高,点A到树的距离AD为21米,将一长为2米的标杆BE在与点A相距3米的点B处垂直立于地面,此时,观察视线恰好经过标杆顶点E及树的顶点C,求树CD的高.
如图,某人在点A处测量树高,点A到树的距离AD为21米,将一长为2米的标杆BE在与点A相距3米的点B处垂直立于地面,此时,观察视线恰好经过标杆顶点E及树的顶点C,求树CD的高. 如图所示,长方形内有两个相邻的正方形,面积分别为3和5,那么阴影部分的面积为$\sqrt{15}$-3.
如图所示,长方形内有两个相邻的正方形,面积分别为3和5,那么阴影部分的面积为$\sqrt{15}$-3.