题目内容
在平面直角坐标系中，△OAB与△OA′B′是以O为位似中心的位似图形，A点坐标为（4，-2），A点的对应点A′的坐标为（-2，1），B点坐标为（6，-4），则B′的坐标为 ．
考点：位似变换,坐标与图形性质
专题：
分析：利用已知对应点的坐标变化规律得出位似比为：-
，进而得出对应点B′点坐标．
| 1 |
| 2 |
解答：解：∵△OAB与△OA′B′是以O为位似中心的位似图形，A点坐标为（4，-2），A点的对应点A′的坐标为（-2，1），
∴B点坐标为（6，-4），则B′的坐标为：（-3，2）．
故答案为：（-3，2）．
∴B点坐标为（6，-4），则B′的坐标为：（-3，2）．
故答案为：（-3，2）．
点评：此题主要考查了位似变换与坐标与图形的性质，得出位似比是解题关键．
练习册系列答案
浙江名校名师金卷系列答案
全优冲刺100分系列答案
相关题目
已知x2+kxy+16y2是一个完全平方式，则k的值是（ ）
| A、8 | B、±8 | C、16 | D、±16 |
一个可以改变体积的密闭容器内装有一定质量的某种气体，当改变容器体积时，气体的密度也随之改变．密度ρ（单位：kg/m3）与体积V（单位：m3）满足函数关系式ρ=| k |
| V |
| A、ρ≤1.5kg/m3 |
| B、0kg/m3＜ρ＜1.5kg/m3 |
| C、ρ≥1.5kg/m3 |
| D、ρ＞1.5kg/m3 |
如图所示，在宽为20m，长为32m的矩形地面上，修筑同样宽的三条道路，（互相垂直），余下部分作为耕地，耕地面积为570m2，如果设修建道路的宽为x m，则x满足的方程是（ ）| A、2x2-52x+32=0 |
| B、x2-52x+64=0 |
| C、x2-36x+35=0 |
| D、x2-36x-35=0 |
如图，PA，PB分别与⊙O相切于A，B两点，点E在 |
| AB |
| A、3cm | B、6cm |
| C、9cm | D、12cm |
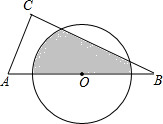如图，在△ABC中，∠C=90°，AB=6，AC=3，O为AB中点，则半径为