题目内容
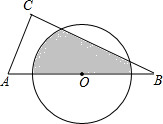 如图,在△ABC中,∠C=90°,AB=6,AC=3,O为AB中点,则半径为
如图,在△ABC中,∠C=90°,AB=6,AC=3,O为AB中点,则半径为| 3 |
| 2 |
| 2 |
考点:扇形面积的计算
专题:计算题
分析:⊙O交BC于E、F,交AB于M、N,作OH⊥EF于H,连结OE、OF,如图,先根据含30度的直角三角形三边的关系得到∠B=30°,且OB=
AB=3,在Rt△BOH中,利用∠B=30°得到OH=
OB=
,∠BOH=60°,接着在Rt△OHF中利用勾股定理计算出HF=
,于是可判断△OHF为等腰直角三角形,所以∠HOF=45°,根据等腰三角形的性质,由OH⊥EF得到∠EOH=∠FOH=45°,EH=FH=
,则可计算出∠NOF=15°,∠MOE=75°,然后根据扇形的面积公式和圆心落在点O的圆形纸片能盖住△ABC的部分面积=S扇形MOE+S△EOF+S扇形NOF进行计算.
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
解答:解:⊙O交BC于E、F,交AB于M、N,作OH⊥EF于H,连结OE、OF,如图,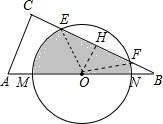
∵∠C=90°,AB=6,AC=3,
∴∠B=30°,
∵O为AB中点,
∴OB=
AB=3,
在Rt△BOH中,∵∠B=30°
∴OH=
OB=
,∠BOH=60°,
在Rt△OHF中,∵OF=
,OH=
,
∴HF=
=
,
∴△OHF为等腰直角三角形,
∴∠HOF=45°,
∵OH⊥EF,
∴∠EOH=∠FOH=45°,EH=FH=
,
∴∠NOF=60°-45°=15°,
∴∠MOE=90°-15°=75°,
∴圆心落在点O的圆形纸片能盖住△ABC的部分面积=S扇形MOE+S△EOF+S扇形NOF
=
+
•3•
+
=
π+
.
故答案为
π+
.

∵∠C=90°,AB=6,AC=3,
∴∠B=30°,
∵O为AB中点,
∴OB=
| 1 |
| 2 |
在Rt△BOH中,∵∠B=30°
∴OH=
| 1 |
| 2 |
| 3 |
| 2 |
在Rt△OHF中,∵OF=
3
| ||
| 2 |
| 3 |
| 2 |
∴HF=
| OF2-OH2 |
| 3 |
| 2 |
∴△OHF为等腰直角三角形,
∴∠HOF=45°,
∵OH⊥EF,
∴∠EOH=∠FOH=45°,EH=FH=
| 3 |
| 2 |
∴∠NOF=60°-45°=15°,
∴∠MOE=90°-15°=75°,
∴圆心落在点O的圆形纸片能盖住△ABC的部分面积=S扇形MOE+S△EOF+S扇形NOF
=
75•π•(
| ||||
| 360 |
| 1 |
| 2 |
| 3 |
| 2 |
15•π•(
| ||||
| 360 |
=
| 9 |
| 8 |
| 9 |
| 4 |
故答案为
| 9 |
| 8 |
| 9 |
| 4 |
点评:本题考查了扇形面积的计算:设圆心角是n°,圆的半径为R的扇形面积为S,则S扇形=
πR2或S扇形=
lR(其中l为扇形的弧长).求阴影面积的主要思路是将不规则图形面积转化为规则图形的面积.
| 360 |
| n |
| 1 |
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2014年上半年,怀柔国税局累计入库消费税11000多万元,将11000用科学记数法表示应为( )
| A、1.1×104 |
| B、1.1×103 |
| C、11×103 |
| D、0.11×105 |
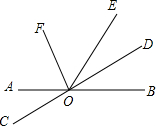 如图,直线AB,CD相交于点O,OD平分∠BOE,OF平分∠AOE.
如图,直线AB,CD相交于点O,OD平分∠BOE,OF平分∠AOE.
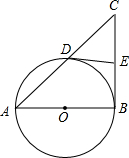 如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,点E是BC的中点.求证:DE是⊙O的切线.
如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,点E是BC的中点.求证:DE是⊙O的切线.