规定:用{M}表示大于M的最小整数.例如{$\frac{5}{2}$}=3.{5}=6.{-1.3}=-1等,用[M]表示不大于M的最大整数.例如[$\frac{7}{2}$]=3.[4]=4.[-1.5]=-2.如果整数x满足关系式:{x}2+4[x]=17.则x=-8或2．题目和参考答案——青夏教育精英家教网—

题目内容

20．规定：用{M}表示大于M的最小整数，例如{$\frac{5}{2}$}=3，{5}=6，{-1.3}=-1等；用[M]表示不大于M的最大整数，例如[$\frac{7}{2}$]=3，[4]=4，[-1.5]=-2，如果整数x满足关系式：{x}²+4[x]=17，则x=-8或2．

分析根据新定义得到（x+1）²+4x=17，然后把方程化为一般式后利用因式分解法解方程．

解答解：∵{x}²+4[x]=17，
∴（x+1）²+4x=17，
整理得x²+6x-16=0，
（x+8）（x-2）=0，
x+8=0或x-2=0，
所以x₁=-8，x₂=2．
即x的值为-8或2．
故答案为-8或2．

点评本题考查了解一元二次方程-因式分解法：先把方程的右边化为0，再把左边通过因式分解化为两个一次因式的积的形式，那么这两个因式的值就都有可能为0，这就能得到两个一元一次方程的解，这样也就把原方程进行了降次，把解一元二次方程转化为解一元一次方程的问题了（数学转化思想）．

练习册系列答案

相关题目

3．

如图，已知BD，CE分别为∠ABC，∠ACB的平分线，AM⊥CE于M，AN⊥BD于N．求证：MN=$\frac{1}{2}$（AB+AC-BC）．

11．

如图是两块完全一样的含30°角的三角板，分别记作△ABC和△A₁B₁C₁，现将两块三角板重叠在一起，高较长直角边的中点为M，绕中点M转动上面的三角板ABC，直角顶点C恰好落在三角板△A₁B₁C₁的斜边A₁B₁上．当∠A=30°，B₁C=2时，则此时AB的长为（　　）

8．已知等边△ABC的边长为4，P是△ABC内一点，且点P在BC的垂直平分线上，若PA=$\sqrt{3}$，则PB长为（　　）

15．实验证明，平面镜反射光线的规律是：射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等．如图1，一束光线m射到平面镜a上，被a反射后的光线为n，则入射光线m、反射光线n与平面镜a所夹的锐角∠1=∠2．
（1）利用这个规律人们制作了潜望镜，图2是潜望镜工作原理示意图，AB、CD是平行放置的两面平面镜．已知光线经过平面镜反射时，有∠1=∠2，∠3=∠4，请解释进入潜望镜的光线m为什么和离开潜望镜的光线n是平行的？（请把证明过程补充完整）
理由：
∵AB∥CD（已知），
∴∠2=∠3 （两直线平行，内错角相等　）
∵∠1=∠2，∠3=∠4（已知），
∴∠1=∠2=∠3=∠4（等量代换），
∴180°-∠1-∠2=180°-∠3-∠4（等量减等量，差相等），
即：∠5=∠6（等量代换），
∴m∥n．（内错角相等，两直线平行）
（2）显然，改变两面平面镜AB、CD之间的位置关系，经过两次反射后，入射光线m与反射光线n之间的位置关系会随之改变，请你猜想：图3中，当两平面镜AB、CD的夹角∠ABC=90°时，仍可以使入射光线m与反射光线n平行但方向相反．（直接写出结果）

5．

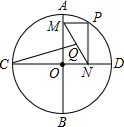如图，⊙O的半径为2，AB，CD是互相垂直的两条直径，点P是⊙O上任意一点（P与A，B，C，D不重合），过点P作PM⊥AB于点M，PN⊥CD于点N，点Q是MN的中点，当点P沿着圆周转过45°时，点Q走过的路径长为$\frac{π}{4}$．

12．

在矩形ABCD中，BC=4，BG与对角线AC垂直且分别交AC，AD及射线CD于点E，F，G，当点F为AD中点时，∠ECF的正切值是（　　）

$\frac{{\sqrt{2}}}{4}$

D．

$\frac{{2\sqrt{2}}}{3}$

9．

如图，MN是半径为4cm的⊙O的直径，点A在⊙O上，∠AMN=30°，点B为劣弧AN的中点．点P是直径MN上一动点，则PA+PB的最小值为4$\sqrt{2}$．

10．若矩形ABCD∽矩形EFGH，相似比为2：3，已知AB=3cm，BC=5cm，则矩形EFGH的周长是（　　）

试题分类