题目内容
12. 在矩形ABCD中,BC=4,BG与对角线AC垂直且分别交AC,AD及射线CD于点E,F,G,当点F为AD中点时,∠ECF的正切值是( )
在矩形ABCD中,BC=4,BG与对角线AC垂直且分别交AC,AD及射线CD于点E,F,G,当点F为AD中点时,∠ECF的正切值是( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{2}}}{4}$ | D. | $\frac{{2\sqrt{2}}}{3}$ |
分析 由在矩形ABCD中,BC=4,点F为AD中点,可求得AF=2,易证得△AEF∽△CEB,由相似三角形的对应边成比例,可得BF=3FE,继而求得答案.
解答 解:∵点F为AD中点,且AD=BC=4,
∴AF=$\frac{1}{2}$AD=2,
∵矩形ABCD中,AD∥BC,
∴△AEF∽△CEB,
∴$\frac{AE}{CE}$=$\frac{FE}{BE}$=$\frac{AF}{CB}$=$\frac{2}{4}$=$\frac{1}{2}$,
∴CE=2AE,BE=2FE,
∴AC=3AE,BF=3FE,
∵F为AD的中点,由对称性,得到BF=CF,
∴$\frac{EF}{CF}$=$\frac{EF}{BF}$=$\frac{1}{3}$
∴CF=3EF
∴EC2=FC2-EF2=9EF2-EF2=8EF2
∴EC=2$\sqrt{2}$EF
∴tan∠ECF=$\frac{EF}{EC}$=$\frac{EF}{2\sqrt{2}EF}$=$\frac{\sqrt{2}}{4}$.
故选:C.
点评 此题考查了相似三角形的判定与性质、矩形的性质以及三角函数的定义,掌握三角形相似的判定与性质是解决问题的关键.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
1.在下列长度的四组线段中,不能组成直角三角形的是( )
| A. | 3,4,5 | B. | 5,12,13 | C. | 1,1,$\sqrt{2}$ | D. | 4,5,6 |
 如图,正方形ABCD中,点M为DA延长线上一点,连接BM,过点C作CN∥BM,交AD于点N,在CD延长线上取一点F,使BM=CF-DN,连接BF,交CN于点E.
如图,正方形ABCD中,点M为DA延长线上一点,连接BM,过点C作CN∥BM,交AD于点N,在CD延长线上取一点F,使BM=CF-DN,连接BF,交CN于点E. 如图,在△ABC中,DE∥BC,DF∥AB,D,E,M分别为AC,AB,BE的中点,连接DM,以DM为边作△DMN,连接FN,且DM=DN.若∠B=∠C=∠MDN=60°,AB=6,则FN的长度为$\frac{3}{2}$.
如图,在△ABC中,DE∥BC,DF∥AB,D,E,M分别为AC,AB,BE的中点,连接DM,以DM为边作△DMN,连接FN,且DM=DN.若∠B=∠C=∠MDN=60°,AB=6,则FN的长度为$\frac{3}{2}$.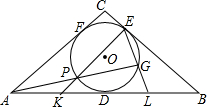 在等腰△ABC中,AC=BC,其内切圆分别与边AB、BC、CA切于点D、E、F.一条过点A且异于AE的直线交△ABC的内切圆于点P、G,EP、EG分别交AB于点K、L.求证:DK=DL.
在等腰△ABC中,AC=BC,其内切圆分别与边AB、BC、CA切于点D、E、F.一条过点A且异于AE的直线交△ABC的内切圆于点P、G,EP、EG分别交AB于点K、L.求证:DK=DL. 如图,在△ABE中∠AEB=90°,AB=$\sqrt{26}$,以AB为边在△ABE的同侧作正方形ABCD,点O为AC与BD的交点,连接OE,OE=2$\sqrt{2}$,点P为AB上一点,将△APE沿直线PE翻折得到△GPE,若PG⊥BE于点F,则BF=5-$\frac{5\sqrt{26}}{26}$.
如图,在△ABE中∠AEB=90°,AB=$\sqrt{26}$,以AB为边在△ABE的同侧作正方形ABCD,点O为AC与BD的交点,连接OE,OE=2$\sqrt{2}$,点P为AB上一点,将△APE沿直线PE翻折得到△GPE,若PG⊥BE于点F,则BF=5-$\frac{5\sqrt{26}}{26}$.