题目内容

10．若矩形ABCD∽矩形EFGH，相似比为2：3，已知AB=3cm，BC=5cm，则矩形EFGH的周长是（　　）
A．16cmB．12cmC．24cmD．36cm

分析 根据题意求出矩形ABCD的周长，根据相似三角形的周长之比等于相似比求出周长之比，计算即可．

解答 解：∵AB=3cm，BC=5cm，
∴矩形ABCD的周长=2×（3+5）=16cm，
∵矩形ABCD∽矩形EFGH，相似比为2：3，
∴矩形ABCD与矩形EFGH的周长比2：3，
∴矩形EFGH的周长为24cm，
故选：C．

点评 本题考查的是相似多边形的性质，掌握相似多边形对应边之比、周长之比等于相似比，而面积之比等于相似比的平方是解题的关键．

练习册系列答案
相关题目
20．规定：用{M}表示大于M的最小整数，例如{$\frac{5}{2}$}=3，{5}=6，{-1.3}=-1等；用[M]表示不大于M的最大整数，例如[$\frac{7}{2}$]=3，[4]=4，[-1.5]=-2，如果整数x满足关系式：{x}2+4[x]=17，则x=-8或2．
1．在下列长度的四组线段中，不能组成直角三角形的是（　　）
A．3，4，5B．5，12，13C．1，1，$\sqrt{2}$D．4，5，6
18．已知关于x的一元二次方程x2-（m+1）x+$\frac{1}{4}{m^2}$+1=0的两根是一个矩形的两邻边的长，且矩形的对角线长为$\sqrt{29}$，则m的值是2．
5．计算：
①1-$\frac{1}{3}$×（-3）2；
②-$\frac{1}{2}$+1$\frac{1}{5}$-2$\frac{7}{10}$；
③-2$\frac{1}{2}$+5$\frac{3}{5}$÷（-2）×（-$\frac{5}{14}$）；
④（-5）×（-3$\frac{2}{5}$）-（-7）×3$\frac{2}{5}$+12×（-3$\frac{2}{5}$）．
15．方程2x2-ax+7=0，有一根是$\frac{1}{2}$，则另一根为（　　）
A．7B．7.5C．-7D．15
2．（a+b-c）（-c-a-b）=c2-（a+b）2．
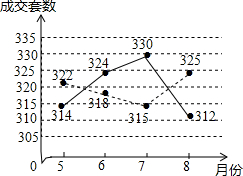19．当今社会，住房问题是百姓较为关心的一个话题，某市的相关部门对该市汉江区和新洲区20135-8月的商品住房成交套数进行数据统计，并将汉江区和新洲区所统计的数据绘制车折线统计图（如图所示，图中实线表示的是汉江区的数据，虚线表示的是新洲区的数据）．
（1）汉江、新洲两区商品住房成交套数的数据的中位数分别是319、320；
（2）通过计算判断5月到8月，哪个区所销售的商品住房的业绩更稳定？
（3）为了提升两区商品住房的销售业绩，汉江区和新洲区决定联合举行“买房大酬宾”活动，该活动内容为：在汉江区购买A，B或C型的任意一种住房后，再在新洲区购买D，E或F型的任意一种住房时，可享受九折的优惠．小李家正好想在汉江和新洲两区各购买一套住房，请用画树状图法或列表法求出所购买的两套住房恰好是A型和E型的概率．
20．计算：sin60°+|-5|-$\sqrt{3}$×（2014-π）0+${（-1）}^{2014}+（\frac{2}{\sqrt{3}-1}）^{-1}$=5$\frac{1}{2}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网