题目内容
15.实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.如图1,一束光线m射到平面镜a上,被a反射后的光线为n,则入射光线m、反射光线n与平面镜a所夹的锐角∠1=∠2.(1)利用这个规律人们制作了潜望镜,图2是潜望镜工作原理示意图,AB、CD是平行放置的两面平面镜.已知光线经过平面镜反射时,有∠1=∠2,∠3=∠4,请解释进入潜望镜的光线m为什么和离开潜望镜的光线n是平行的?(请把证明过程补充完整)
理由:
∵AB∥CD(已知),
∴∠2=∠3 (两直线平行,内错角相等 )
∵∠1=∠2,∠3=∠4(已知),
∴∠1=∠2=∠3=∠4(等量代换),
∴180°-∠1-∠2=180°-∠3-∠4(等量减等量,差相等),
即:∠5=∠6(等量代换),
∴m∥n.(内错角相等,两直线平行)
(2)显然,改变两面平面镜AB、CD之间的位置关系,经过两次反射后,入射光线m与反射光线n之间的位置关系会随之改变,请你猜想:图3中,当两平面镜AB、CD的夹角∠ABC=90°时,仍可以使入射光线m与反射光线n平行但方向相反.(直接写出结果)

分析 (1)求出∠5=∠6,根据平行线的判定得出即可;
(2)根据三角形内角和定理求出∠2+∠3=90°,求出∠EAC+∠FCA=180°,根据平行线的判定得出即可.
解答  (1)证明:如图2,∵AB∥CD(已知),
(1)证明:如图2,∵AB∥CD(已知),
∴∠2=∠3 (两直线平行,内错角相等),
∵∠1=∠2,∠3=∠4(已知),
∴∠1=∠2=∠3=∠4(等量代换),
∴180°-∠1-∠2=180°-∠3-∠4(等量减等量,差相等),
即:∠5=∠6(等量代换),
∴m∥n (内错角相等,两直线平行).
故答案为:两直线平行,内错角相等,∠5=∠6,m∥n,内错角相等,两直线平行;
(2)∠ABC=90°,
理由是:如图3,∵∠ABC=90°,
∴∠2+∠3=180°-90°=90°,
∵∠1=∠2,∠3=∠4(已知),
∴∠1+∠2+∠3+∠4=80°,
∴∠EAC+∠FCA=180°+180°-180°=180°,
∴AE∥CF.
故答案为:90.
点评 本题考查了平行线的性质和判定的应用,能灵活运用定理进行推理是解此题的关键.

练习册系列答案
相关题目
 如图,在四边形ABCD中,AO是∠DAB的平分线,BO是∠ABC的平分线,AO与BO交于点O.若∠C+∠D=120°,求∠AOB的度数.
如图,在四边形ABCD中,AO是∠DAB的平分线,BO是∠ABC的平分线,AO与BO交于点O.若∠C+∠D=120°,求∠AOB的度数.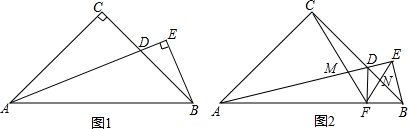
 如图,正方形ABCD中,点M为DA延长线上一点,连接BM,过点C作CN∥BM,交AD于点N,在CD延长线上取一点F,使BM=CF-DN,连接BF,交CN于点E.
如图,正方形ABCD中,点M为DA延长线上一点,连接BM,过点C作CN∥BM,交AD于点N,在CD延长线上取一点F,使BM=CF-DN,连接BF,交CN于点E. 如图,在平面直角坐标系中,四边形OABC是边长为8的正方形,M(8,m)、N(n,8)分别是线段AB、BC上的两个动点,且ON⊥MN,当OM最小时,m+n=10.
如图,在平面直角坐标系中,四边形OABC是边长为8的正方形,M(8,m)、N(n,8)分别是线段AB、BC上的两个动点,且ON⊥MN,当OM最小时,m+n=10. 如图,在△ABC中,DE∥BC,DF∥AB,D,E,M分别为AC,AB,BE的中点,连接DM,以DM为边作△DMN,连接FN,且DM=DN.若∠B=∠C=∠MDN=60°,AB=6,则FN的长度为$\frac{3}{2}$.
如图,在△ABC中,DE∥BC,DF∥AB,D,E,M分别为AC,AB,BE的中点,连接DM,以DM为边作△DMN,连接FN,且DM=DN.若∠B=∠C=∠MDN=60°,AB=6,则FN的长度为$\frac{3}{2}$. 如图,在△ABE中∠AEB=90°,AB=$\sqrt{26}$,以AB为边在△ABE的同侧作正方形ABCD,点O为AC与BD的交点,连接OE,OE=2$\sqrt{2}$,点P为AB上一点,将△APE沿直线PE翻折得到△GPE,若PG⊥BE于点F,则BF=5-$\frac{5\sqrt{26}}{26}$.
如图,在△ABE中∠AEB=90°,AB=$\sqrt{26}$,以AB为边在△ABE的同侧作正方形ABCD,点O为AC与BD的交点,连接OE,OE=2$\sqrt{2}$,点P为AB上一点,将△APE沿直线PE翻折得到△GPE,若PG⊥BE于点F,则BF=5-$\frac{5\sqrt{26}}{26}$.