题目内容
9. 如图,MN是半径为4cm的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN的中点.点P是直径MN上一动点,则PA+PB的最小值为4$\sqrt{2}$.
如图,MN是半径为4cm的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN的中点.点P是直径MN上一动点,则PA+PB的最小值为4$\sqrt{2}$.
分析 如图作点A关于MN的对称点A′,连接A′B交MN于P,此时PA+PB最小,且此时PA+PB=BA′,只要证明△BOA′是直角三角形即可解决问题.
解答 解:如图,作点A关于MN的对称点A′,连接A′B交MN于P,此时PA+PB最小,连接OB、OA′. ∵PA=PA′,
∵PA=PA′,
∴PA+PB=PA′+PB=BA′,
∵∠AMN=30°,点B是AM弧中点,
∴∠BOM=∠AMN=30°,
∵∠AMN=∠A′MN=30°,OB=OA′,
∴∠OMA=∠OA′M=30°,
∴∠NOA′=∠OMA′+∠OA′M=60°,
∴∠BOA′=90°,
∴A$′B=\sqrt{2}OB$=4$\sqrt{2}$,
∴PA+PB的最小值=4$\sqrt{2}$.
故答案为4$\sqrt{2}$.
点评 本题考查最短问题、圆的有关知识,利用对称是解决最短问题的关键,在求线段BA′时猜想线段BA′是不是特殊三角形的边,把问题转化为求特殊三角形的边的问题,属于中考常考题型.

练习册系列答案
相关题目
14. 如图,正方形ABCD和正方形DEFG的顶点在y轴上,顶点D、F在x轴上,点C在DE边上,反比例函数y=$\frac{k}{x}$(k≠0)的图象经过B,C和边EF的中点M,若S四边形ABCD=8,则正方形DEFG的面积是( )
如图,正方形ABCD和正方形DEFG的顶点在y轴上,顶点D、F在x轴上,点C在DE边上,反比例函数y=$\frac{k}{x}$(k≠0)的图象经过B,C和边EF的中点M,若S四边形ABCD=8,则正方形DEFG的面积是( )
 如图,正方形ABCD和正方形DEFG的顶点在y轴上,顶点D、F在x轴上,点C在DE边上,反比例函数y=$\frac{k}{x}$(k≠0)的图象经过B,C和边EF的中点M,若S四边形ABCD=8,则正方形DEFG的面积是( )
如图,正方形ABCD和正方形DEFG的顶点在y轴上,顶点D、F在x轴上,点C在DE边上,反比例函数y=$\frac{k}{x}$(k≠0)的图象经过B,C和边EF的中点M,若S四边形ABCD=8,则正方形DEFG的面积是( )| A. | $\frac{23}{9}$ | B. | $\frac{128}{9}$ | C. | 16 | D. | $\frac{15}{4}$ |
1.在下列长度的四组线段中,不能组成直角三角形的是( )
| A. | 3,4,5 | B. | 5,12,13 | C. | 1,1,$\sqrt{2}$ | D. | 4,5,6 |
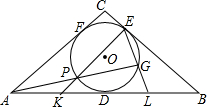 在等腰△ABC中,AC=BC,其内切圆分别与边AB、BC、CA切于点D、E、F.一条过点A且异于AE的直线交△ABC的内切圆于点P、G,EP、EG分别交AB于点K、L.求证:DK=DL.
在等腰△ABC中,AC=BC,其内切圆分别与边AB、BC、CA切于点D、E、F.一条过点A且异于AE的直线交△ABC的内切圆于点P、G,EP、EG分别交AB于点K、L.求证:DK=DL. 如图,在△ABE中∠AEB=90°,AB=$\sqrt{26}$,以AB为边在△ABE的同侧作正方形ABCD,点O为AC与BD的交点,连接OE,OE=2$\sqrt{2}$,点P为AB上一点,将△APE沿直线PE翻折得到△GPE,若PG⊥BE于点F,则BF=5-$\frac{5\sqrt{26}}{26}$.
如图,在△ABE中∠AEB=90°,AB=$\sqrt{26}$,以AB为边在△ABE的同侧作正方形ABCD,点O为AC与BD的交点,连接OE,OE=2$\sqrt{2}$,点P为AB上一点,将△APE沿直线PE翻折得到△GPE,若PG⊥BE于点F,则BF=5-$\frac{5\sqrt{26}}{26}$.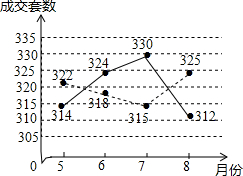 当今社会,住房问题是百姓较为关心的一个话题,某市的相关部门对该市汉江区和新洲区20135-8月的商品住房成交套数进行数据统计,并将汉江区和新洲区所统计的数据绘制车折线统计图(如图所示,图中实线表示的是汉江区的数据,虚线表示的是新洲区的数据).
当今社会,住房问题是百姓较为关心的一个话题,某市的相关部门对该市汉江区和新洲区20135-8月的商品住房成交套数进行数据统计,并将汉江区和新洲区所统计的数据绘制车折线统计图(如图所示,图中实线表示的是汉江区的数据,虚线表示的是新洲区的数据).