题目内容
5.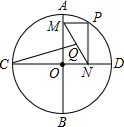 如图,⊙O的半径为2,AB,CD是互相垂直的两条直径,点P是⊙O上任意一点(P与A,B,C,D不重合),过点P作PM⊥AB于点M,PN⊥CD于点N,点Q是MN的中点,当点P沿着圆周转过45°时,点Q走过的路径长为$\frac{π}{4}$.
如图,⊙O的半径为2,AB,CD是互相垂直的两条直径,点P是⊙O上任意一点(P与A,B,C,D不重合),过点P作PM⊥AB于点M,PN⊥CD于点N,点Q是MN的中点,当点P沿着圆周转过45°时,点Q走过的路径长为$\frac{π}{4}$.
分析 根据OP的长度不变,始终等于半径,则根据矩形的性质可得OQ=1,再由走过的角度代入弧长公式即可.
解答 解:∵PM⊥AB于点M,PN⊥CD于点N,
∴四边形ONPM是矩形,
又∵点Q为MN的中点,
∴点Q为OP的中点,又OP=2,
则OQ=1,
点Q走过的路径长=$\frac{45×π×1}{180}$=$\frac{π}{4}$.
故答案为:$\frac{π}{4}$.
点评 本题考查了弧长的计算及矩形的性质,解答本题的关键是根据矩形的性质得出点Q运动轨迹的半径,要求同学们熟练掌握弧长的计算公式.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
16.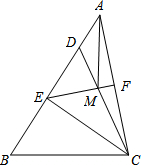 如图,在△ABC中,点D在AB上,且CD=CB,点E为BD的中点,点F为AC的中点,连结EF交CD于点M,连接AM.若∠BAC=45°,AM=4,DM=3,则BC的长度为( )
如图,在△ABC中,点D在AB上,且CD=CB,点E为BD的中点,点F为AC的中点,连结EF交CD于点M,连接AM.若∠BAC=45°,AM=4,DM=3,则BC的长度为( )
 如图,在△ABC中,点D在AB上,且CD=CB,点E为BD的中点,点F为AC的中点,连结EF交CD于点M,连接AM.若∠BAC=45°,AM=4,DM=3,则BC的长度为( )
如图,在△ABC中,点D在AB上,且CD=CB,点E为BD的中点,点F为AC的中点,连结EF交CD于点M,连接AM.若∠BAC=45°,AM=4,DM=3,则BC的长度为( )| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
14. 如图,正方形ABCD和正方形DEFG的顶点在y轴上,顶点D、F在x轴上,点C在DE边上,反比例函数y=$\frac{k}{x}$(k≠0)的图象经过B,C和边EF的中点M,若S四边形ABCD=8,则正方形DEFG的面积是( )
如图,正方形ABCD和正方形DEFG的顶点在y轴上,顶点D、F在x轴上,点C在DE边上,反比例函数y=$\frac{k}{x}$(k≠0)的图象经过B,C和边EF的中点M,若S四边形ABCD=8,则正方形DEFG的面积是( )
 如图,正方形ABCD和正方形DEFG的顶点在y轴上,顶点D、F在x轴上,点C在DE边上,反比例函数y=$\frac{k}{x}$(k≠0)的图象经过B,C和边EF的中点M,若S四边形ABCD=8,则正方形DEFG的面积是( )
如图,正方形ABCD和正方形DEFG的顶点在y轴上,顶点D、F在x轴上,点C在DE边上,反比例函数y=$\frac{k}{x}$(k≠0)的图象经过B,C和边EF的中点M,若S四边形ABCD=8,则正方形DEFG的面积是( )| A. | $\frac{23}{9}$ | B. | $\frac{128}{9}$ | C. | 16 | D. | $\frac{15}{4}$ |
15.方程2x2-ax+7=0,有一根是$\frac{1}{2}$,则另一根为( )
| A. | 7 | B. | 7.5 | C. | -7 | D. | 15 |
 如图,AB是⊙O的直径,弦CD与AB相交于点E.
如图,AB是⊙O的直径,弦CD与AB相交于点E.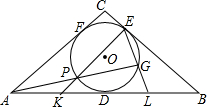 在等腰△ABC中,AC=BC,其内切圆分别与边AB、BC、CA切于点D、E、F.一条过点A且异于AE的直线交△ABC的内切圆于点P、G,EP、EG分别交AB于点K、L.求证:DK=DL.
在等腰△ABC中,AC=BC,其内切圆分别与边AB、BC、CA切于点D、E、F.一条过点A且异于AE的直线交△ABC的内切圆于点P、G,EP、EG分别交AB于点K、L.求证:DK=DL.