题目内容
9.先化简,再求值:$\frac{{x}^{2}+2x+1}{x+2}$÷$\frac{{x}^{2}-1}{x-1}$-$\frac{x}{x+2}$,其中x是不等式组$\left\{\begin{array}{l}{2-(x-1)≥2x}\\{\frac{2x-5}{3}-x≤-1}\end{array}\right.$的整数解.分析 先根据分式混合运算的法则把原式进行化简,再求出x的值代入进行计算即可.
解答 解:原式=$\frac{(x+1)^{2}}{x+2}$•$\frac{1}{x+1}$-$\frac{x}{x+2}$
=$\frac{x+1}{x+2}$-$\frac{x}{x+2}$
=$\frac{1}{x+2}$,
解不等式组$\left\{\begin{array}{l}2-(x-1)≥2x\\ \frac{2x-5}{3}-x≤-1\end{array}\right.$得,-2≤x≤1,
当x=0时,原式=$\frac{1}{2}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.若分式$\frac{2x-y}{{3{x^2}y}}$的x和y均扩大为原来各自的10倍,则分式的值( )
| A. | 不变 | B. | 缩小到原分式值的$\frac{1}{10}$ | ||
| C. | 缩小到原分式值的$\frac{1}{100}$ | D. | 缩小到原分式值的$\frac{1}{1000}$ |
20.据英国每日邮报报道,目前,科学家发现地球上迄今为止最大的病毒,它被称为“潜多拉病毒”,直径为0.001毫米,是普通病毒直径的10倍,仅有6%的基因类似于地球上的其他生物体.0.001毫米用科学记数法应表示为( )
| A. | 1×10-3米 | B. | 1×10-4米 | C. | 1×10-6米 | D. | 1×10-7米 |
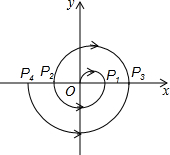 如图,在平面直角坐标系中,设一动点P自原点O处开始顺时针运动,沿半径为1个单位长度的半圆运动至x轴,记为点P1;再沿半径为2个单位长度的半圆运动至x轴,记为点P2;再沿半径为3个单位长度的半圆运动至x轴,记为点P3,…如此继续运动下去,当点P运动到点P302处时,点P所运动的路程为45753π.(结果保留π)
如图,在平面直角坐标系中,设一动点P自原点O处开始顺时针运动,沿半径为1个单位长度的半圆运动至x轴,记为点P1;再沿半径为2个单位长度的半圆运动至x轴,记为点P2;再沿半径为3个单位长度的半圆运动至x轴,记为点P3,…如此继续运动下去,当点P运动到点P302处时,点P所运动的路程为45753π.(结果保留π) 如图,⊙O的直径AB=10,CD是⊙O的弦,AC与BD相交于点P.
如图,⊙O的直径AB=10,CD是⊙O的弦,AC与BD相交于点P.