题目内容
18. 如图,⊙O的直径AB=10,CD是⊙O的弦,AC与BD相交于点P.
如图,⊙O的直径AB=10,CD是⊙O的弦,AC与BD相交于点P.(1)判断△APB与△DPC是否相似?并说明理由;
(2)若CE⊥BD于E,且PE:EC=3:4,求弦CD的长.
分析 (1)根据圆周角定理得到∠D=∠A,∠DCA=∠B,由相似三角形的判定定理即可得到结论;
(2)连接BC,设PE=3x,CE=4x,根据勾股定理得到PC=5x,由三角函数的定义得到cos∠BPC=$\frac{PE}{PC}$=$\frac{3}{5}$,求得cos∠BPC=$\frac{PC}{PB}$=$\frac{3}{5}$,根据相似三角形的性质即可得到结论.
解答 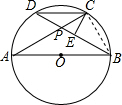 解:(1)△APB与△DPC相似,
解:(1)△APB与△DPC相似,
∵∠D=∠A,∠DCA=∠B,
∴△APB∽△DPC;
(2)连接BC,∵CE⊥BD于E,且PE:EC=3:4,
∴设PE=3x,CE=4x,
∴PC=5x,
∴cos∠BPC=$\frac{PE}{PC}$=$\frac{3}{5}$,
∵AB是⊙O的直径,
∴∠PCB=90°,
∴cos∠BPC=$\frac{PC}{PB}$=$\frac{3}{5}$,
∵△APB∽△CDP,
∴$\frac{CD}{AB}=\frac{PC}{PB}$=$\frac{3}{5}$,
∵AB=10,
∴CD=6.
点评 该题主要考查了圆周角定理及其推论、相似三角形的判定及其性质等重要数学知识点及其应用问题;牢固掌握定理是基础,科学解答是关键;对综合的分析问题解决问题的能力提出了较高的要求.

练习册系列答案
相关题目
6. 如图,已知△ADB≌△CBD,AB=4,BD=6,BC=3,则△ADB的周长是( )
如图,已知△ADB≌△CBD,AB=4,BD=6,BC=3,则△ADB的周长是( )
 如图,已知△ADB≌△CBD,AB=4,BD=6,BC=3,则△ADB的周长是( )
如图,已知△ADB≌△CBD,AB=4,BD=6,BC=3,则△ADB的周长是( )| A. | 12 | B. | 13 | C. | 14 | D. | 15 |
3.在平面直角坐标系中,抛物线y=x2+2x-3与x轴的交点个数是( )
| A. | 0个 | B. | 1 个 | C. | 2个 | D. | 3个 |
10.某水资源保护组织对石家庄某小区的居民进行节约水资源的问卷调查.某居民在问卷上的选项代号画“√”,这个过程是收集数据中的( )
| A. | 确定调查范围 | B. | 汇总调查数据 | C. | 实施调查 | D. | 明确调查问题 |
8.在下列四个图案中既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,AD是△ABC的外角平分线,交BC的延长线于D点,若∠B=30°,∠ACD=100°,求∠DAE的度数.
如图,AD是△ABC的外角平分线,交BC的延长线于D点,若∠B=30°,∠ACD=100°,求∠DAE的度数.