题目内容
14.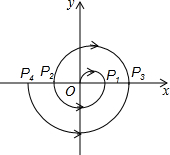 如图,在平面直角坐标系中,设一动点P自原点O处开始顺时针运动,沿半径为1个单位长度的半圆运动至x轴,记为点P1;再沿半径为2个单位长度的半圆运动至x轴,记为点P2;再沿半径为3个单位长度的半圆运动至x轴,记为点P3,…如此继续运动下去,当点P运动到点P302处时,点P所运动的路程为45753π.(结果保留π)
如图,在平面直角坐标系中,设一动点P自原点O处开始顺时针运动,沿半径为1个单位长度的半圆运动至x轴,记为点P1;再沿半径为2个单位长度的半圆运动至x轴,记为点P2;再沿半径为3个单位长度的半圆运动至x轴,记为点P3,…如此继续运动下去,当点P运动到点P302处时,点P所运动的路程为45753π.(结果保留π)
分析 结合图形可知动点P运动过的每一段均为半圆,根据圆的周长公式可得知每段的路程长度,将各段相加后即可得出结论.
解答 解:由运动规则可知,P点运动的每一段均为半圆,圆的周长C=2πr(r为半径).
结合题意可知:O到P1路程为π,P1到P2路程为2π,…,P300到P301路程为301π,P301到P302路程为302π,
故当点P运动到点P302处时,点P所运动的路程为(1+2+3+…+301+302)π.
∵1+302=2+301=3+300=…=151+152,
∴1+2+3+…+302=$\frac{302}{2}$×(1+302)=45753.
故答案为:45753π.
点评 本题考查了弧长的计算公式以及数的变化规律,解题的关键是找出“1+302=2+301=3+300=…=151+152”这个规律.本题属于基础题,难度不大,但对于初中生来说没有学到等差数列的求和公式,故不能直接应用,需对具体数据具体分析.

练习册系列答案
相关题目
4.用配方法解方程2x2-4x+1=0时,配方后所得的方程为( )
| A. | (x-2)2=3 | B. | 2(x-2)2=3 | C. | 2(x-1)2=1 | D. | $2{({x-1})^2}=\frac{1}{2}$ |
6. 如图,已知△ADB≌△CBD,AB=4,BD=6,BC=3,则△ADB的周长是( )
如图,已知△ADB≌△CBD,AB=4,BD=6,BC=3,则△ADB的周长是( )
 如图,已知△ADB≌△CBD,AB=4,BD=6,BC=3,则△ADB的周长是( )
如图,已知△ADB≌△CBD,AB=4,BD=6,BC=3,则△ADB的周长是( )| A. | 12 | B. | 13 | C. | 14 | D. | 15 |
3.在平面直角坐标系中,抛物线y=x2+2x-3与x轴的交点个数是( )
| A. | 0个 | B. | 1 个 | C. | 2个 | D. | 3个 |
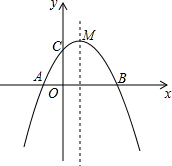 如图,抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,且OA=OC,M是抛物线的顶点,三角形AMB的面积等于1,则下列结论:
如图,抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,且OA=OC,M是抛物线的顶点,三角形AMB的面积等于1,则下列结论: 将一张三角形纸片ABC,沿AD进行折叠,点C的对应点E落在△ABC外面,DE交AB于点F,得到如图所示的多边形AEFBD,这个多边形的面积是△ABC面积的$\frac{13}{16}$.已知图中阴影部分的面积为50,则△ABC的面积为80.
将一张三角形纸片ABC,沿AD进行折叠,点C的对应点E落在△ABC外面,DE交AB于点F,得到如图所示的多边形AEFBD,这个多边形的面积是△ABC面积的$\frac{13}{16}$.已知图中阴影部分的面积为50,则△ABC的面积为80.