题目内容

17．如图，将一张正六边形纸片的阴影部分剪下，拼成一个四边形．若拼成的四边形的面积为2a，则纸片的剩余部分的面积为4a．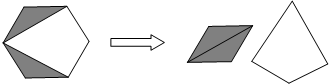

分析 如图所示可将正六边形分为6个全等的三角形，阴影部分由两个三角形组成，剩余部分由4个三角形组成，故此可求得剩余部分的面积．

解答 解：如图所示：

将正六边形可分为6个全等的三角形，
∵阴影部分的面积为2a，
∴每一个三角形的面积为a，
∵剩余部分可分割为4个三角形，
∴剩余部分的面积为4a．
故答案为：4a．

点评 本题主要考查的是图形的剪拼，将正六边形分割为六个全等的三角形是解题的关键．

练习册系列答案
相关题目
7．某中学开展“校园文化节“活动，对学生参加书法比赛的作品按A、B、C、D四个等级进行了评定．现随机抽取部分参赛学生书法作品的评定结果进行统计分析，并将分析结果绘制成如图扇形统计图（图①）和条形统计图（图②），根据所给信息完成下列问题：
（1）本次抽取的样本的容量为120；
（2）在图①中，C级所对应的扇形圆心角度数是108°；
（3）请在图②中将条形统计图补充完整；
（4）已知该校本次活动学生参赛的书法作品共750件，请你估算参赛作品中A级和B级作品共多少件？
8．有这样一道试题：“先化简，再求值：$（{\frac{x-2}{x+2}+\frac{4x}{{{x^2}-4}}}）÷\frac{1}{{{x^2}-4}}$其中$x=-\sqrt{3}$．”马虎做该题时把“$x=-\sqrt{3}$”错抄成“$x=\sqrt{3}$”，但他的计算结果却是正确的，你能解释一下其中的原因吗？
5．已知$\frac{x}{4}$=$\frac{y}{3}$=$\frac{z}{5}$，且$\sqrt{y+4}$=z-x，则x的值为16．
12．将2×2的正方形网格如图所示的放置在平面直角坐标系中，每个小正方形的顶点称为格点，每个小正方形的边长都是1，正方形ABCD的顶点都在格点上，若直线y=kx（k≠0）与正方形ABCD有公共点，则k不可能是（　　）
A．3B．2C．1D．$\frac{1}{2}$
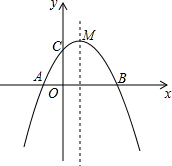2．如图，抛物线y=ax2+bx+c与x轴交于A、B两点，与y轴交于点C，且OA=OC，M是抛物线的顶点，三角形AMB的面积等于1，则下列结论：
①$\frac{{b}^{2}-4ac}{4a}$＜0  ②ac-b+1=0  ③（2-b）3=8a2  ④OA•OB=-$\frac{c}{a}$
其中正确的结论的个数是（　　）
A．4B．3C．2D．1
9．先化简，再求值：$\frac{{x}^{2}+2x+1}{x+2}$÷$\frac{{x}^{2}-1}{x-1}$-$\frac{x}{x+2}$，其中x是不等式组$\left\{\begin{array}{l}{2-（x-1）≥2x}\\{\frac{2x-5}{3}-x≤-1}\end{array}\right.$的整数解．
6．如图，已知△ADB≌△CBD，AB=4，BD=6，BC=3，则△ADB的周长是（　　）
A．12B．13C．14D．15
7．在△ABC中，∠A=∠C，点E在BC边上，过点E作射线EF∥AB交AC于点F，EM交AC于点M，点N在射线EF上，且∠EMN=∠ENM，设∠ABC=α，∠MEN=β．
（1）如图1，若点M在线段AF上，α=80°，β=30°，求∠FMN的度数；
（2）若点M在AC边上（不与点A、C、F重合），α、β为任意角度，探究∠FMN与α、β的数量关系，请在图2中画出图形，然后直接写出答案．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网