题目内容
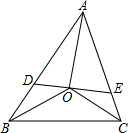 已知,如图,在△ABC中,∠ABC、∠ACB的平分线相交于点O,过O作AO的垂线分别交于AB,AC于点D,E,求证:∠OBC=∠EOC.
已知,如图,在△ABC中,∠ABC、∠ACB的平分线相交于点O,过O作AO的垂线分别交于AB,AC于点D,E,求证:∠OBC=∠EOC.考点:等腰三角形的判定与性质
专题:
分析:由BO与CO是∠ABC、∠ACB的平分线,可得AO是∠BAC的平分线,利用三角形的内角和可得∠BOC=180°-
∠ABC-
∠ACB=180°-
(∠ABC+∠ACB)又因为∠ABC+∠ACB=180°-∠BAC,所以可得∠BOC=180°-
(180°-∠BAC)=90°+
∠BAC,再利用外角的性质可得∠OEC=90°+
∠BAC,又因为∠ECO=∠BCO,即可证明△OBC∽△EOC,从而证得∠OBC=∠EOC.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:证明:∵∠ABC、∠ACB的平分线相交于点O,
∴AO平分是∠BAC的平分线,
∴∠OAE=
∠BAC,
∵OB、OC分别平分∠ABC和∠ACB,
∴∠OBC=
∠ABC,∠OCB=
∠ACB,
∴∠BOC=180°-∠OBC-∠OCB
=180°-
(∠ABC+∠ACB)
∵∠ABC+∠ACB=180°-∠BAC,
∴∠BOC=180°-
(180°-∠BAC)
=90°+
∠BAC,
∵AO⊥DE,
∴∠AOE=90°,
∴∠OEC=∠AOE+∠OAE=90°+
∠BAC,
∴∠BOC=∠OEC,
又∵∠ECO=∠OCB,
∴△BOC∽△OEC,
∴∠OBC=∠EOC.
∴AO平分是∠BAC的平分线,
∴∠OAE=
| 1 |
| 2 |
∵OB、OC分别平分∠ABC和∠ACB,
∴∠OBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BOC=180°-∠OBC-∠OCB
=180°-
| 1 |
| 2 |
∵∠ABC+∠ACB=180°-∠BAC,
∴∠BOC=180°-
| 1 |
| 2 |
=90°+
| 1 |
| 2 |
∵AO⊥DE,
∴∠AOE=90°,
∴∠OEC=∠AOE+∠OAE=90°+
| 1 |
| 2 |
∴∠BOC=∠OEC,
又∵∠ECO=∠OCB,
∴△BOC∽△OEC,
∴∠OBC=∠EOC.
点评:本题主要考查角平分线的性质,三角形的内角和,相似三角形的判定和性质,能通过图形和已知找到角之间的关系是解题的关键.

练习册系列答案
相关题目
某次抽奖活动在三个箱子中均有红、黄两种颜色的球各一个,奖励规则如下:从三个箱子中分别摸出一个球,摸出的3个球均为红球的得一等奖;摸出的三个球中只有两个红球的得二等奖;摸出的3个球只有1个红球的得三等奖;其余情况没有奖,则不中奖的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,AB是⊙O的直径,弦CD⊥AB,若∠C=30°,CD=2
如图,AB是⊙O的直径,弦CD⊥AB,若∠C=30°,CD=2| 3 |
| A、π | ||||
| B、2π | ||||
C、
| ||||
D、
|
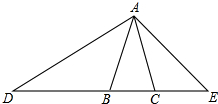 如图,已知等腰△ABC中,AB=AC=2,点D在边BC的反向延长线上,且DB=3,点E在边BC的延长线上,且∠EAC=∠D.
如图,已知等腰△ABC中,AB=AC=2,点D在边BC的反向延长线上,且DB=3,点E在边BC的延长线上,且∠EAC=∠D.
 已知:如图,AB•AD=AC•AE,求证:△ABC∽△AED.
已知:如图,AB•AD=AC•AE,求证:△ABC∽△AED. 在边长为a的菱形ABCD中,∠DAB=60°,E是AD上异于A,D两点的动点,F是CD上的动点,满足AE+CF=a
在边长为a的菱形ABCD中,∠DAB=60°,E是AD上异于A,D两点的动点,F是CD上的动点,满足AE+CF=a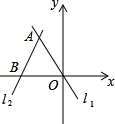 如图,已知:A(-1,2),S△AOB=
如图,已知:A(-1,2),S△AOB= 如图,AC⊥BD,AC=DC,BC=EC,连接DE并延长交AB于F,求证:DF⊥AB.
如图,AC⊥BD,AC=DC,BC=EC,连接DE并延长交AB于F,求证:DF⊥AB.