题目内容
某次抽奖活动在三个箱子中均有红、黄两种颜色的球各一个,奖励规则如下:从三个箱子中分别摸出一个球,摸出的3个球均为红球的得一等奖;摸出的三个球中只有两个红球的得二等奖;摸出的3个球只有1个红球的得三等奖;其余情况没有奖,则不中奖的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:列表法与树状图法
专题:
分析:首先根据题意画出树状图,然后由树状图求得所有等可能的结果与不中奖的情况,再利用概率公式即可求得答案.
解答:解:画树状图得:

∵共有8种等可能的结果,不中奖的有1种情况,
∴不中奖的概率是:
.
故选A.

∵共有8种等可能的结果,不中奖的有1种情况,
∴不中奖的概率是:
| 1 |
| 8 |
故选A.
点评:此题考查了树状图法与列表法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
根式
中x的取值范围是( )
| 2-x |
| A、x≥2 | B、x≤2 |
| C、x<2 | D、x>2 |
 如图,在△ABC中取一点P,使得CP=CB,求证:AB>AP.
如图,在△ABC中取一点P,使得CP=CB,求证:AB>AP.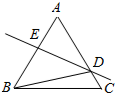 如图,等腰△ABC中,已知AB=AC,∠A=30°,AB的重直平分线交AC于D,交AB于E,求CBD的度数.
如图,等腰△ABC中,已知AB=AC,∠A=30°,AB的重直平分线交AC于D,交AB于E,求CBD的度数. 表示运算:x+y+z,
表示运算:x+y+z, 表示运算a-b+c-d,求
表示运算a-b+c-d,求 ×
× 的值.
的值.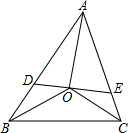 已知,如图,在△ABC中,∠ABC、∠ACB的平分线相交于点O,过O作AO的垂线分别交于AB,AC于点D,E,求证:∠OBC=∠EOC.
已知,如图,在△ABC中,∠ABC、∠ACB的平分线相交于点O,过O作AO的垂线分别交于AB,AC于点D,E,求证:∠OBC=∠EOC.