题目内容
 在边长为a的菱形ABCD中,∠DAB=60°,E是AD上异于A,D两点的动点,F是CD上的动点,满足AE+CF=a
在边长为a的菱形ABCD中,∠DAB=60°,E是AD上异于A,D两点的动点,F是CD上的动点,满足AE+CF=a(1)求证:△BDE≌△BCF;
(2)证明:不论E、F怎样移动,△BEF总是等边三角形.
(3)设△BEF的面积为S,求S的取值范围.
考点:菱形的性质,全等三角形的判定与性质,等边三角形的判定与性质
专题:
分析:(1)利用菱形的性质和正三角形的特点进行证明;
(2)△BEF为正三角形,可解用(1)全等的结论证明;
(3)作出恰当的辅助线,构成直角三角形,根据直角三角形的特点和三角函数进行计算.
(2)△BEF为正三角形,可解用(1)全等的结论证明;
(3)作出恰当的辅助线,构成直角三角形,根据直角三角形的特点和三角函数进行计算.
解答: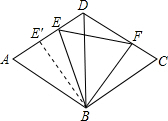 (1)证明:∵四边形ABCD是菱形,
(1)证明:∵四边形ABCD是菱形,
∴AB=AD.
又∵∠DAB=60°,
∴△ABD是等边三角形,
∴BD=AD,
∵菱形ABCD的边长为a,
∴BD=a,
∴△ABD和△BCD都为正三角形,
∴∠BDE=∠BCF=60°,BD=BC,
∵AE+DE=AD=a,而AE+CF=a,
∴DE=CF.
在△BDE与△BCF中,
,
∴△BDE≌△BCF(SAS);
(2)解:△BEF为正三角形.
理由:∵△BDE≌△BCF,
∴∠DBE=∠CBF,BE=BF,
∵∠DBC=∠DBF+∠CBF=60°,
∴∠DBF+∠DBE=60°即∠EBF=60°,
∴△BEF为正三角形;
(3)解:设BE=BF=EF=x,
则S=
•x•x•sin60°=
x2,
当BE⊥AD时,x最小=a×sin60°=
a,
∴S最小=
×(
a)2=
a2,
当BE与AB重合时,x最大=a,
∴S最大=
×a2=
a2,
∴
a2≤S≤
a2.
 (1)证明:∵四边形ABCD是菱形,
(1)证明:∵四边形ABCD是菱形,∴AB=AD.
又∵∠DAB=60°,
∴△ABD是等边三角形,
∴BD=AD,
∵菱形ABCD的边长为a,
∴BD=a,
∴△ABD和△BCD都为正三角形,
∴∠BDE=∠BCF=60°,BD=BC,
∵AE+DE=AD=a,而AE+CF=a,
∴DE=CF.
在△BDE与△BCF中,
|
∴△BDE≌△BCF(SAS);
(2)解:△BEF为正三角形.
理由:∵△BDE≌△BCF,
∴∠DBE=∠CBF,BE=BF,
∵∠DBC=∠DBF+∠CBF=60°,
∴∠DBF+∠DBE=60°即∠EBF=60°,
∴△BEF为正三角形;
(3)解:设BE=BF=EF=x,
则S=
| 1 |
| 2 |
| ||
| 4 |
当BE⊥AD时,x最小=a×sin60°=
| ||
| 2 |
∴S最小=
| ||
| 4 |
| ||
| 2 |
3
| ||
| 16 |
当BE与AB重合时,x最大=a,
∴S最大=
| ||
| 4 |
| ||
| 4 |
∴
3
| ||
| 16 |
| ||
| 4 |
点评:本题考查的是菱形的面积求法及菱形性质的综合运用、等边三角形的判定与性质以及全等三角形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
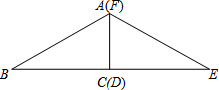 如图,Rt△ABC≌Rt△FED,其中∠BCA=∠EDF=90°,∠B=∠E=30°,AC=FD=
如图,Rt△ABC≌Rt△FED,其中∠BCA=∠EDF=90°,∠B=∠E=30°,AC=FD=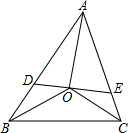 已知,如图,在△ABC中,∠ABC、∠ACB的平分线相交于点O,过O作AO的垂线分别交于AB,AC于点D,E,求证:∠OBC=∠EOC.
已知,如图,在△ABC中,∠ABC、∠ACB的平分线相交于点O,过O作AO的垂线分别交于AB,AC于点D,E,求证:∠OBC=∠EOC.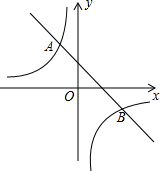 已知:如图,一次函数y=kx+b的图象与反比例函数y=
已知:如图,一次函数y=kx+b的图象与反比例函数y=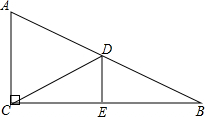 如上图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC的垂直平分线交AB于点D,垂足为E.
如上图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC的垂直平分线交AB于点D,垂足为E. 小颖将手中的一副三角尺按如图所示摆放在一起,连接AD后,你能帮他求出∠ADB的正切值吗?
小颖将手中的一副三角尺按如图所示摆放在一起,连接AD后,你能帮他求出∠ADB的正切值吗? 如图,点O在直线AB上,∠AOD沿直线OD翻折得到∠COD,OE是∠BOC的平分线,说明OD⊥OE的理由.
如图,点O在直线AB上,∠AOD沿直线OD翻折得到∠COD,OE是∠BOC的平分线,说明OD⊥OE的理由.