题目内容
 如图,AB是⊙O的直径,弦CD⊥AB,若∠C=30°,CD=2
如图,AB是⊙O的直径,弦CD⊥AB,若∠C=30°,CD=2| 3 |
| A、π | ||||
| B、2π | ||||
C、
| ||||
D、
|
考点:扇形面积的计算,勾股定理,垂径定理
专题:
分析:根据垂径定理求得CE=ED=
,然后由圆周角定理知∠DOE=60°,然后通过解直角三角形求得线段OD、OE的长度,最后将相关线段的长度代入S阴影=S扇形ODA-S△DOE+S△AEC.
| 3 |
解答:解:∵AB是⊙O的直径,弦CD⊥AB,
∴CE=ED=
,
又∵∠DCA=30°,
∴∠DOE=2∠CDB=60°,∠ODE=30°,
∴OE=DE•cot60°=
×
=1,OD=2OE=2,
∴S阴影=S扇形ODA-S△DOE+S△AEC=
-
OE×ED+
AE•EC=
-
+
=
.
故选C.
∴CE=ED=
| 3 |
又∵∠DCA=30°,
∴∠DOE=2∠CDB=60°,∠ODE=30°,
∴OE=DE•cot60°=
| 3 |
| ||
| 3 |
∴S阴影=S扇形ODA-S△DOE+S△AEC=
| 60π×OC2 |
| 360 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2π |
| 3 |
| ||
| 2 |
| ||
| 2 |
| 2π |
| 3 |
故选C.
点评:本题考查的是扇形面积的计算,通过解直角三角形得到相关线段的长度是解答本题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
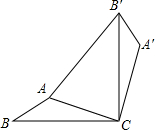 如图,在△ABC中,AB=1,AC=2,现将△ABC绕点C顺时针旋转90°得到△A′B′C′,连接AB′,并有AB′=3,则∠A′的度数为( )
如图,在△ABC中,AB=1,AC=2,现将△ABC绕点C顺时针旋转90°得到△A′B′C′,连接AB′,并有AB′=3,则∠A′的度数为( )| A、125° | B、130° |
| C、135° | D、140° |
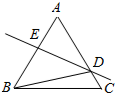 如图,等腰△ABC中,已知AB=AC,∠A=30°,AB的重直平分线交AC于D,交AB于E,求CBD的度数.
如图,等腰△ABC中,已知AB=AC,∠A=30°,AB的重直平分线交AC于D,交AB于E,求CBD的度数.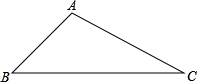 如图,在△ABC中,∠B=45°,∠C=15°,BC=5
如图,在△ABC中,∠B=45°,∠C=15°,BC=5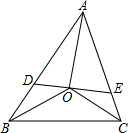 已知,如图,在△ABC中,∠ABC、∠ACB的平分线相交于点O,过O作AO的垂线分别交于AB,AC于点D,E,求证:∠OBC=∠EOC.
已知,如图,在△ABC中,∠ABC、∠ACB的平分线相交于点O,过O作AO的垂线分别交于AB,AC于点D,E,求证:∠OBC=∠EOC.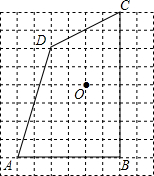 如图,在9×9网络图中,每个正方形边长均为1,点O和四边形ABCD的顶点均为小正方形的顶点.
如图,在9×9网络图中,每个正方形边长均为1,点O和四边形ABCD的顶点均为小正方形的顶点.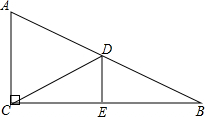 如上图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC的垂直平分线交AB于点D,垂足为E.
如上图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC的垂直平分线交AB于点D,垂足为E.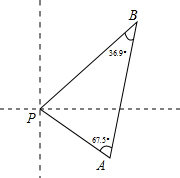 我南海巡逻船接到有人落水求救信号,如图,巡逻船A观测到∠PAB=67.5°,同时,巡逻船B观测到∠PBA=36.9°,两巡逻船相距63海里,求此时巡逻船A与落水人P的距离?(参考数据:sin36.9°≈
我南海巡逻船接到有人落水求救信号,如图,巡逻船A观测到∠PAB=67.5°,同时,巡逻船B观测到∠PBA=36.9°,两巡逻船相距63海里,求此时巡逻船A与落水人P的距离?(参考数据:sin36.9°≈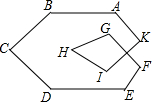 如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I+∠K的度数为
如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I+∠K的度数为