题目内容
 如图,AC⊥BD,AC=DC,BC=EC,连接DE并延长交AB于F,求证:DF⊥AB.
如图,AC⊥BD,AC=DC,BC=EC,连接DE并延长交AB于F,求证:DF⊥AB.考点:全等三角形的判定与性质
专题:证明题
分析:如图,运用SAS公理证明△DCE≌△ACB,得到∠A=∠D;结合∠A+∠B=90°,即可解决问题.
解答: 证明:如图,∵AC⊥BD,
证明:如图,∵AC⊥BD,
∴∠ECD=∠BCA;
在△DCE与△ACB中,
,
∴△DCE≌△ACB(SAS),
∴∠A=∠D;
∵∠A+∠B=90°,
∴∠D+∠B=90°,
∴∠DFB=90°,即DF⊥AB.
 证明:如图,∵AC⊥BD,
证明:如图,∵AC⊥BD,∴∠ECD=∠BCA;
在△DCE与△ACB中,
|
∴△DCE≌△ACB(SAS),
∴∠A=∠D;
∵∠A+∠B=90°,
∴∠D+∠B=90°,
∴∠DFB=90°,即DF⊥AB.
点评:该题考查了全等三角形的判定、应用问题;观察图形,数形结合,找出图中隐含的相等或全等关系是解题的关键.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
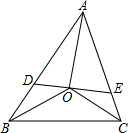 已知,如图,在△ABC中,∠ABC、∠ACB的平分线相交于点O,过O作AO的垂线分别交于AB,AC于点D,E,求证:∠OBC=∠EOC.
已知,如图,在△ABC中,∠ABC、∠ACB的平分线相交于点O,过O作AO的垂线分别交于AB,AC于点D,E,求证:∠OBC=∠EOC. 如图,点O在直线AB上,∠AOD沿直线OD翻折得到∠COD,OE是∠BOC的平分线,说明OD⊥OE的理由.
如图,点O在直线AB上,∠AOD沿直线OD翻折得到∠COD,OE是∠BOC的平分线,说明OD⊥OE的理由. 如图,设∠XOY=α
如图,设∠XOY=α
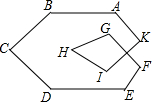 如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I+∠K的度数为
如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I+∠K的度数为 如图,AC平分∠DAB,∠1=∠2,试说明AB与CD的位置关系,并予以证明.
如图,AC平分∠DAB,∠1=∠2,试说明AB与CD的位置关系,并予以证明.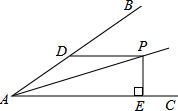 若∠BAC=30°,AP平分∠BAC,PD∥AC且PD=5,PE⊥AC于E,则PE=
若∠BAC=30°,AP平分∠BAC,PD∥AC且PD=5,PE⊥AC于E,则PE=