题目内容
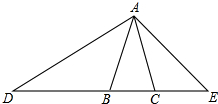如图，已知等腰△ABC中，AB=AC=2，点D在边BC的反向延长线上，且DB=3，点E在边BC的延长线上，且∠EAC=∠D．（1）求线段CE的长；
（2）求证：
| AC2 |
| AE2 |
| BD |
| BE |
（3）当AC平分∠BAE时，求线段AD的长．
考点：相似三角形的判定与性质,等腰三角形的性质
专题：
分析：（1）根据条件可证明△ACE∽△DBA，利用相似三角形的对应边成比例可求得CE；
（2）可证明△DBA∽△DAE，可得
=
=
，根据相似三角形的性质解答即可．
（2）可证明△DBA∽△DAE，可得
| CA |
| CD |
| AB |
| DA |
| AB |
| DA |
解答：解：（1）∵AB=AC，
∴∠ABC=∠ACB，
∴∠ABD=∠ACE．
∵∠EAC=∠D，
∴△DBA∽△ACE，
∴
=
，
∵AB=AC=2，DB=3，
∴
=
，
∴CE=
；
（2）∵△ACE∽△ADB，
∴
=
，
∴AC2=BD•CE，
∵∠ACE=∠D+∠BAD+∠BAC，∠DAE=∠DAB+∠BAC+∠CAE，
∴∠ACE=∠DAE且∠E=∠E，
∴△ACE∽△DAE，
∴
=
，
∴AE2=ED•CE，
∴
=
．
（3）∵AC平分∠BAE，
∴∠EAC=∠CAB
．
∵∠EAC=∠D，
∴∠CAB=∠D．
∵∠ACB=∠ACB，
∴△CAB∽△CDA，
∴
=
=
，
∴
=
，
即3+
x2-
=x，
解得x1=4，x2=-1（舍去），
即AD=4．
∴∠ABC=∠ACB，
∴∠ABD=∠ACE．
∵∠EAC=∠D，
∴△DBA∽△ACE，
∴
| DB |
| AC |
| AB |
| CE |
∵AB=AC=2，DB=3，
∴
| 3 |
| 2 |
| 2 |
| CE |
∴CE=
| 4 |
| 3 |
（2）∵△ACE∽△ADB，
∴
| AC |
| BD |
| CE |
| AB |
∴AC2=BD•CE，
∵∠ACE=∠D+∠BAD+∠BAC，∠DAE=∠DAB+∠BAC+∠CAE，
∴∠ACE=∠DAE且∠E=∠E，
∴△ACE∽△DAE，
∴
| AE |
| DE |
| CE |
| AE |
∴AE2=ED•CE，
∴
| AC2 |
| AE2 |
| BD |
| DE |
（3）∵AC平分∠BAE，
∴∠EAC=∠CAB
．∵∠EAC=∠D，
∴∠CAB=∠D．
∵∠ACB=∠ACB，
∴△CAB∽△CDA，
∴
| CA |
| CD |
| AB |
| DA |
| AB |
| DA |
∴
| 2 |
| 3+y |
| 2 |
| x |
即3+
| 1 |
| 3 |
| 13 |
| 3 |
解得x1=4，x2=-1（舍去），
即AD=4．
点评：本题考查了相似三角形的判定与性质和等腰三角形的性质，熟悉图形的特点，从中找到相关图形是解题的关键．
练习册系列答案
相关题目
根式
中x的取值范围是（ ）
| 2-x |
| A、x≥2 | B、x≤2 |
| C、x＜2 | D、x＞2 |
表示运算：x+y+z，
表示运算a-b+c-d，求
×
的值．
光线由上到下照射一个三棱柱时的正投影如图所示，三棱柱的高为10，请分别画出三棱柱的各个侧面的正投影，并标出投影的边长．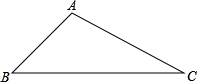
如图，在△ABC中，∠B=45°，∠C=15°，BC=5
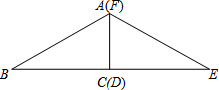如图，Rt△ABC≌Rt△FED，其中∠BCA=∠EDF=90°，∠B=∠E=30°，AC=FD=
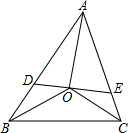已知，如图，在△ABC中，∠ABC、∠ACB的平分线相交于点O，过O作AO的垂线分别交于AB，AC于点D，E，求证：∠OBC=∠EOC．
如图，点O在直线AB上，∠AOD沿直线OD翻折得到∠COD，OE是∠BOC的平分线，说明OD⊥OE的理由．