题目内容
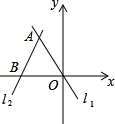 如图,已知:A(-1,2),S△AOB=
如图,已知:A(-1,2),S△AOB=| 5 |
| 3 |
考点:两条直线相交或平行问题
专题:计算题
分析:先利用三角形面积公式计算OB得到B点坐标,然后利用待定系数法分别求两直线解析式.
解答:解:∵S△AOB=
,
∴
×2×OB=
,
∴OB=
,
∴B(-
,0),
设直线l1的解析式为y=kx,
把A(-1,2)代入得-k=2,解得k=-2,
所以直线l1的解析式为y=-2x;
设直线l2的解析式为y=mx+n,
把A(-1,2)、B(-
,0)分别代入得
,
解得
,
所以直线l2的解析式为y=3x+5.
| 5 |
| 3 |
∴
| 1 |
| 2 |
| 5 |
| 3 |
∴OB=
| 5 |
| 3 |
∴B(-
| 5 |
| 3 |
设直线l1的解析式为y=kx,
把A(-1,2)代入得-k=2,解得k=-2,
所以直线l1的解析式为y=-2x;
设直线l2的解析式为y=mx+n,
把A(-1,2)、B(-
| 5 |
| 3 |
|
解得
|
所以直线l2的解析式为y=3x+5.
点评:本题考查了两条直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么它们的自变量系数相同,即k值相同.也考查了待定系数法求一次函数解析式.

练习册系列答案
相关题目
 表示运算:x+y+z,
表示运算:x+y+z, 表示运算a-b+c-d,求
表示运算a-b+c-d,求 ×
× 的值.
的值.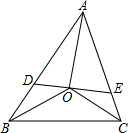 已知,如图,在△ABC中,∠ABC、∠ACB的平分线相交于点O,过O作AO的垂线分别交于AB,AC于点D,E,求证:∠OBC=∠EOC.
已知,如图,在△ABC中,∠ABC、∠ACB的平分线相交于点O,过O作AO的垂线分别交于AB,AC于点D,E,求证:∠OBC=∠EOC.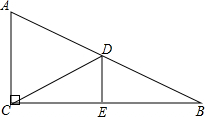 如上图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC的垂直平分线交AB于点D,垂足为E.
如上图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC的垂直平分线交AB于点D,垂足为E. 小颖将手中的一副三角尺按如图所示摆放在一起,连接AD后,你能帮他求出∠ADB的正切值吗?
小颖将手中的一副三角尺按如图所示摆放在一起,连接AD后,你能帮他求出∠ADB的正切值吗?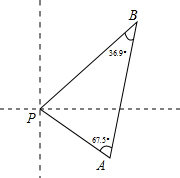 我南海巡逻船接到有人落水求救信号,如图,巡逻船A观测到∠PAB=67.5°,同时,巡逻船B观测到∠PBA=36.9°,两巡逻船相距63海里,求此时巡逻船A与落水人P的距离?(参考数据:sin36.9°≈
我南海巡逻船接到有人落水求救信号,如图,巡逻船A观测到∠PAB=67.5°,同时,巡逻船B观测到∠PBA=36.9°,两巡逻船相距63海里,求此时巡逻船A与落水人P的距离?(参考数据:sin36.9°≈ 如图,点O在直线AB上,∠AOD沿直线OD翻折得到∠COD,OE是∠BOC的平分线,说明OD⊥OE的理由.
如图,点O在直线AB上,∠AOD沿直线OD翻折得到∠COD,OE是∠BOC的平分线,说明OD⊥OE的理由. 如图,设∠XOY=α
如图,设∠XOY=α 如图,AC平分∠DAB,∠1=∠2,试说明AB与CD的位置关系,并予以证明.
如图,AC平分∠DAB,∠1=∠2,试说明AB与CD的位置关系,并予以证明.