题目内容
13.若二次函数y=ax2+bx+c(a≠0)的图象与x轴有两个交点,坐标分别为(x1,0)、(x2,0),且x1<x2,图象上有一点M(x0,y0),在x轴下方,则下列判断正确的是( )| A. | a(x0-x1)(x0-x2)<0 | B. | a>0 | C. | b2-4ac≥0 | D. | x1<x0<x2 |
分析 由于a的符号不能确定,故应分a>0与a<0进行分类讨论.
解答 解:A、当a>0时,
∵点M(x0,y0),在x轴下方,
∴x1<x0<x2,
∴x0-x1>0,x0-x2<0,
∴a(x0-x1)(x0-x2)<0;
当a<0时,若点M在对称轴的左侧,则x0<x1<x2,
∴x0-x1<0,x0-x2<0,
∴a(x0-x1)(x0-x2)<0;
若点M在对称轴的右侧,则x1<x2<x0,
∴x0-x1>0,x0-x2>0,
∴a(x0-x1)(x0-x2)<0;
综上所述,a(x0-x1)(x0-x2)<0,故本选项正确;
B、a的符号不能确定,故本选项错误;
C、∵函数图象与x轴有两个交点,∴△>0,故本选项错误;
D、x1、x0、x2的大小无法确定,故本选项错误.
故选A.
点评 本题考查的是抛物线与x轴的交点,在解答此题时要注意进行分类讨论.

练习册系列答案
相关题目
1.已知关于x的不等式组$\left\{\begin{array}{l}{2x+m>0}\\{x-1<6}\end{array}\right.$有五个整数解,m的取值范围是( )
| A. | -4≤m<-2 | B. | -4<m<-2 | C. | -4<m≤-2 | D. | -4≤m≤-2 |
18. 如图,正六边形A1B1C1D1E1F1的边长为2,正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切,正六边形A3B3C3D3E3F3的外接圆与正六边形A2B2C2D2E2F2的各边相切,…按这样的规律进行下去,A10B10C10D10E10F10的边长为( )
如图,正六边形A1B1C1D1E1F1的边长为2,正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切,正六边形A3B3C3D3E3F3的外接圆与正六边形A2B2C2D2E2F2的各边相切,…按这样的规律进行下去,A10B10C10D10E10F10的边长为( )
 如图,正六边形A1B1C1D1E1F1的边长为2,正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切,正六边形A3B3C3D3E3F3的外接圆与正六边形A2B2C2D2E2F2的各边相切,…按这样的规律进行下去,A10B10C10D10E10F10的边长为( )
如图,正六边形A1B1C1D1E1F1的边长为2,正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切,正六边形A3B3C3D3E3F3的外接圆与正六边形A2B2C2D2E2F2的各边相切,…按这样的规律进行下去,A10B10C10D10E10F10的边长为( )| A. | $\frac{243}{{2}^{9}}$ | B. | $\frac{81\sqrt{3}}{{2}^{9}}$ | C. | $\frac{81}{{2}^{9}}$ | D. | $\frac{81\sqrt{3}}{{2}^{8}}$ |
2.把所有正奇数从小到大排列,并按如下规律分组:(1),(3,5,7),(9,11,13,15,17),(19,21,23,25,27,29,31),…,现有等式Am=(i,j)表示正奇数m是第i组第j个数(从左往右数),如A7=(2,3),则A2015=( )
| A. | (31,50) | B. | (32,47) | C. | (33,46) | D. | (34,42) |
 如图,在矩形ABCD的对角线AC上取两点E和F,且AE=CF,求证:DF=BE.
如图,在矩形ABCD的对角线AC上取两点E和F,且AE=CF,求证:DF=BE.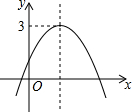 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,且关于x的一元二次方程ax2+bx+c-m=0没有实数根,有下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,且关于x的一元二次方程ax2+bx+c-m=0没有实数根,有下列结论: 《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术.其中,方程术是《九章算术》最高的数学成就.
《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术.其中,方程术是《九章算术》最高的数学成就.