题目内容
8.如果关于x的不等式组$\left\{\begin{array}{l}{5x-α≤0}\\{6x-b>0}\end{array}\right.$的整数解仅为-1,0,1,那么适合这个不等式组的有序实数对(a,b)共有30对.分析 首先解不等式组$\left\{\begin{array}{l}{5x-α≤0}\\{6x-b>0}\end{array}\right.$,则不等式组的解集即可利用a,b表示,根据不等式组的整数解仅为-1,0,1,即可确定a,b的范围,即可确定a,b的整数解,即可求解.
解答 解:由原不等式组可得:$\frac{a}{5}$≤x<$\frac{b}{6}$.
在数轴上画出这个不等式组解集的可能区间,如下图
根据数轴可得:-2<$\frac{a}{5}$≤-1,1<$\frac{b}{6}$≤2.
由:-2<$\frac{a}{5}$≤-1,得-10<a≤-5,
∴a=-9,-8,-7,-6,-5,共5个.
由1<$\frac{b}{6}$≤2得6<b≤12,
∴b=7,8,9,10,11,12,共6个.
5×6=30(个).
故适合这个不等式组的整数a,b的有序数对(a,b)共有30对.
故答案为30.
点评 考查了一元一次不等式组的整数解,注意各个不等式的解集的公式部分就是这个不等式组的解集.但本题是要求整数解的,所以要找出在这范围内的整数.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
18.下列几何体中,俯视图为矩形的是( )
| A. |  | B. |  | C. |  | D. |  |
13.若二次函数y=ax2+bx+c(a≠0)的图象与x轴有两个交点,坐标分别为(x1,0)、(x2,0),且x1<x2,图象上有一点M(x0,y0),在x轴下方,则下列判断正确的是( )
| A. | a(x0-x1)(x0-x2)<0 | B. | a>0 | C. | b2-4ac≥0 | D. | x1<x0<x2 |
20. 在△ABC中,DE∥BC,AE:EC=2:3,DE=4,则BC等于( )
在△ABC中,DE∥BC,AE:EC=2:3,DE=4,则BC等于( )
 在△ABC中,DE∥BC,AE:EC=2:3,DE=4,则BC等于( )
在△ABC中,DE∥BC,AE:EC=2:3,DE=4,则BC等于( )| A. | 10 | B. | 8 | C. | 9 | D. | 6 |
18.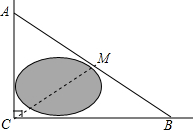 如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开.若测得AM的长为1.2km,则M,C两点间的距离为( )
如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开.若测得AM的长为1.2km,则M,C两点间的距离为( )
 如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开.若测得AM的长为1.2km,则M,C两点间的距离为( )
如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开.若测得AM的长为1.2km,则M,C两点间的距离为( )| A. | 0.5km | B. | 0.6km | C. | 0.9km | D. | 1.2km |

 如图,已知PC平分∠MPN,点O是PC上任意一点,PM与⊙O相切于点E,交PC于A、B两点.
如图,已知PC平分∠MPN,点O是PC上任意一点,PM与⊙O相切于点E,交PC于A、B两点.