题目内容
18. 如图,正六边形A1B1C1D1E1F1的边长为2,正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切,正六边形A3B3C3D3E3F3的外接圆与正六边形A2B2C2D2E2F2的各边相切,…按这样的规律进行下去,A10B10C10D10E10F10的边长为( )
如图,正六边形A1B1C1D1E1F1的边长为2,正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切,正六边形A3B3C3D3E3F3的外接圆与正六边形A2B2C2D2E2F2的各边相切,…按这样的规律进行下去,A10B10C10D10E10F10的边长为( )| A. | $\frac{243}{{2}^{9}}$ | B. | $\frac{81\sqrt{3}}{{2}^{9}}$ | C. | $\frac{81}{{2}^{9}}$ | D. | $\frac{81\sqrt{3}}{{2}^{8}}$ |
分析 连接OE1,OD1,OD2,如图,根据正六边形的性质得∠E1OD1=60°,则△E1OD1为等边三角形,再根据切线的性质得OD2⊥E1D1,于是可得OD2=$\frac{\sqrt{3}}{2}$E1D1=$\frac{\sqrt{3}}{2}$×2,利用正六边形的边长等于它的半径得到正六边形A2B2C2D2E2F2的边长=$\frac{\sqrt{3}}{2}$×2,同理可得正六边形A3B3C3D3E3F3的边长=($\frac{\sqrt{3}}{2}$)2×2,依此规律可得正六边形A10B10C10D10E10F10的边长=($\frac{\sqrt{3}}{2}$)9×2,然后化简即可.
解答  解:连接OE1,OD1,OD2,如图,
解:连接OE1,OD1,OD2,如图,
∵六边形A1B1C1D1E1F1为正六边形,
∴∠E1OD1=60°,
∴△E1OD1为等边三角形,
∵正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切,
∴OD2⊥E1D1,
∴OD2=$\frac{\sqrt{3}}{2}$E1D1=$\frac{\sqrt{3}}{2}$×2,
∴正六边形A2B2C2D2E2F2的边长=$\frac{\sqrt{3}}{2}$×2,
同理可得正六边形A3B3C3D3E3F3的边长=($\frac{\sqrt{3}}{2}$)2×2,
则正六边形A10B10C10D10E10F10的边长=($\frac{\sqrt{3}}{2}$)9×2=$\frac{81\sqrt{3}}{{2}^{8}}$.
故选D.
点评 本题考查了正多边形与圆的关系:把一个圆分成n(n是大于2的自然数)等份,依次连接各分点所得的多边形是这个圆的内接正多边形,这个圆叫做这个正多边形的外接圆.记住正六边形的边长等于它的半径.

| A. | a(x0-x1)(x0-x2)<0 | B. | a>0 | C. | b2-4ac≥0 | D. | x1<x0<x2 |
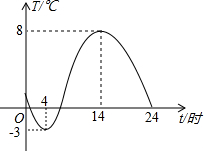 如图,是一台自动测温记录仪的图象,它反映了我市冬季某天气温T随时间t变化而变化的关系,观察图象得到下列信息,其中错误的是( )
如图,是一台自动测温记录仪的图象,它反映了我市冬季某天气温T随时间t变化而变化的关系,观察图象得到下列信息,其中错误的是( )| A. | 凌晨4时气温最低为-3℃ | |
| B. | 14时气温最高为8℃ | |
| C. | 从0时至14时,气温随时间增长而上升 | |
| D. | 从14时至24时,气温随时间增长而下降 |
 如图,已知B、C、E三点在同一条直线上,△ABC与△DCE都是等边三角形,其中线段BD交AC于点G,线段AE交CD于点F,求证:
如图,已知B、C、E三点在同一条直线上,△ABC与△DCE都是等边三角形,其中线段BD交AC于点G,线段AE交CD于点F,求证:
 如图,在△ABC中,DE∥BC,AD:DB=1:2,DE=2,则BC的长是6.
如图,在△ABC中,DE∥BC,AD:DB=1:2,DE=2,则BC的长是6.