题目内容
6.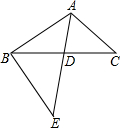 如图,△ABC中,AE交BC于点D,∠C=∠E,AD=4,BC=8,BD:DC=5:3,则DE的长等于( )
如图,△ABC中,AE交BC于点D,∠C=∠E,AD=4,BC=8,BD:DC=5:3,则DE的长等于( )| A. | $\frac{20}{3}$ | B. | $\frac{17}{4}$ | C. | $\frac{16}{3}$ | D. | $\frac{15}{4}$ |
分析 由条件可证明△BDE∽△ADC,且可求得BD和DC的长度,利用相似三角形的对应边的比相等可求得DE.
解答 解:∵∠C=∠E,且∠BDE=∠ADC,
∴△BDE∽△ADC,
∴$\frac{BD}{AD}$=$\frac{DE}{DC}$,
∵BC=8,BD:DC=5:3,
∴BD=5,DC=3,AD=4,
∴$\frac{5}{4}$=$\frac{DE}{3}$,
解得DE=$\frac{15}{4}$,
故选:D.
点评 本题主要考查了相似三角形的判定与性质,解题时注意:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.在△ABC中,AB=13,BC=10,BC边上的中线AD=12,则AC=( )
| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
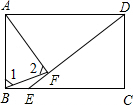 如图,矩形ABCD中,DE交BC于E且DE=AD,AF⊥DE于F,连接BF,求证:∠1=∠2.
如图,矩形ABCD中,DE交BC于E且DE=AD,AF⊥DE于F,连接BF,求证:∠1=∠2.
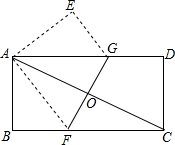 如图,将一矩形纸片ABCD折叠,使两个顶点A,C重合,折痕为FG..若AB=8,BC=16,则△AEG的面积为24.
如图,将一矩形纸片ABCD折叠,使两个顶点A,C重合,折痕为FG..若AB=8,BC=16,则△AEG的面积为24.