题目内容
16.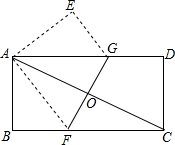 如图,将一矩形纸片ABCD折叠,使两个顶点A,C重合,折痕为FG..若AB=8,BC=16,则△AEG的面积为24.
如图,将一矩形纸片ABCD折叠,使两个顶点A,C重合,折痕为FG..若AB=8,BC=16,则△AEG的面积为24.
分析 先根据折叠的性质求出DG=EG,AE的值,再根据勾股定理可得AG的值,最后根据三角形的面积公式计算.
解答 解:设AG=x,
根据折叠的性质,有DG=EG=16-x,AE=AB=8,
根据勾股定理可得64+(16-x)2=x2,
解得x=10,
EG=16-x=6,
故△AEG的面积为$\frac{1}{2}$•AE•EG=$\frac{1}{2}$×8×6=24.
故答案为:24.
点评 本题通过折叠变换考查学生的逻辑思维能力,解决此类问题,应结合题意,最好实际操作图形的折叠,易于找到图形间的关系.

练习册系列答案
相关题目
6.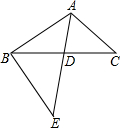 如图,△ABC中,AE交BC于点D,∠C=∠E,AD=4,BC=8,BD:DC=5:3,则DE的长等于( )
如图,△ABC中,AE交BC于点D,∠C=∠E,AD=4,BC=8,BD:DC=5:3,则DE的长等于( )
 如图,△ABC中,AE交BC于点D,∠C=∠E,AD=4,BC=8,BD:DC=5:3,则DE的长等于( )
如图,△ABC中,AE交BC于点D,∠C=∠E,AD=4,BC=8,BD:DC=5:3,则DE的长等于( )| A. | $\frac{20}{3}$ | B. | $\frac{17}{4}$ | C. | $\frac{16}{3}$ | D. | $\frac{15}{4}$ |
6.如图(1),在边长为a的大正方形上剪去一个边长为b的小正方形,可以拼出图(2)所示图形,上述过程可以验证等式( )
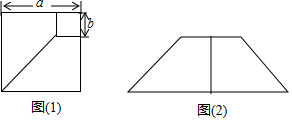

| A. | (a+b)2=a2+2ab+b2 | B. | (a-b)2=a2-2ab+b2 | C. | a2-b2=(a+b)(a-b) | D. | (a+b)2-(a-b)2=4ab |
 如图,∠1+∠2+∠3+∠4+∠5+∠6+∠7=540°.
如图,∠1+∠2+∠3+∠4+∠5+∠6+∠7=540°. 如图,在边长为2的正方形ABCD中,G是AD延长线上的一点,且DG=AD,动点M从A点出发,以每秒1个单位的速度沿着A→C→G的路线向G点匀速运动(M不与A,G重合),设运动时间为t秒,连接BM并延长交AG于N.
如图,在边长为2的正方形ABCD中,G是AD延长线上的一点,且DG=AD,动点M从A点出发,以每秒1个单位的速度沿着A→C→G的路线向G点匀速运动(M不与A,G重合),设运动时间为t秒,连接BM并延长交AG于N. 某型号飞机的机翼形状如图所示,AB∥CD,∠DAE=37°,∠CBE=45°,CD=1.4m,AB、CD之间的距离为5.1m.求AD、AB的长.
某型号飞机的机翼形状如图所示,AB∥CD,∠DAE=37°,∠CBE=45°,CD=1.4m,AB、CD之间的距离为5.1m.求AD、AB的长.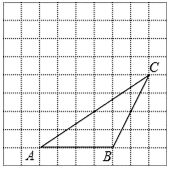 如图,△ABC的顶点都在方格纸的格点上.将△ABC向左平移2格,再向上平移4格.请在图中画出平移后的△A′B′C′,再在图中画出△A′B′C′的高C′D′、中线A′E,若S△BCP=S△ACB,P为异于点B的格点,则点P的个数为4个.
如图,△ABC的顶点都在方格纸的格点上.将△ABC向左平移2格,再向上平移4格.请在图中画出平移后的△A′B′C′,再在图中画出△A′B′C′的高C′D′、中线A′E,若S△BCP=S△ACB,P为异于点B的格点,则点P的个数为4个.