题目内容
6.先化简,再求值:($\frac{6}{x-1}$+$\frac{4}{{x}^{2}-1}$)÷$\frac{3x+5}{x-1}$,其中x=2.分析 先将分式化简,然后代入x的值即可求出答案.
解答 解:当x=2时,
原式=[$\frac{6}{x-1}$+$\frac{4}{(x+1)(x-1)}$]•$\frac{x-1}{3x+5}$
=$\frac{6}{3x+5}$+$\frac{4}{(x+1)(3x+5)}$
=$\frac{6(x+1)}{(3x+5)(x+1)}$+$\frac{4}{(x+1)(3x+5)}$
=$\frac{6x+10}{(x+1)(3x+5)}$
=$\frac{2}{x+1}$
=$\frac{2}{3}$
点评 本题考查分式的化简运算,解题的关键是熟练运用分式的运算法则,本题属于基础题型.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
17.不等式2-3x>7的解为( )
| A. | x>-$\frac{5}{3}$ | B. | x>-$\frac{3}{5}$ | C. | x<-$\frac{5}{3}$ | D. | x<-$\frac{3}{5}$ |
6.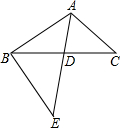 如图,△ABC中,AE交BC于点D,∠C=∠E,AD=4,BC=8,BD:DC=5:3,则DE的长等于( )
如图,△ABC中,AE交BC于点D,∠C=∠E,AD=4,BC=8,BD:DC=5:3,则DE的长等于( )
 如图,△ABC中,AE交BC于点D,∠C=∠E,AD=4,BC=8,BD:DC=5:3,则DE的长等于( )
如图,△ABC中,AE交BC于点D,∠C=∠E,AD=4,BC=8,BD:DC=5:3,则DE的长等于( )| A. | $\frac{20}{3}$ | B. | $\frac{17}{4}$ | C. | $\frac{16}{3}$ | D. | $\frac{15}{4}$ |
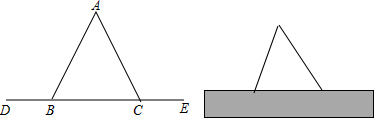
 如图,∠1+∠2+∠3+∠4+∠5+∠6+∠7=540°.
如图,∠1+∠2+∠3+∠4+∠5+∠6+∠7=540°.