题目内容
15．某商店将每件进价为40元的商品按每件60元售出，每天可售出100件，后来经过市场调查发现，这种商品每件的销售价每降低2元其销售量就增加20件，则应将每件降价为多少元时，才能使每天利润为2240元．分析 首先设将每件降价x元时，才能使每天利润为2240元，利用销售量×每件利润=2240元列出方程求解即可．
解答 解：设将每件降价x元时，才能使每天利润为2240元．
则由题意：（60-x-40）（100+x×$\frac{20}{2}$）=2240，
化简得：x2-10x+24=0，
解得x1=4，x2=6，
降价为60-4=56元或60-6=54元．
答：将每件降价为56元或54元时，才能使每天利润为2240元．
点评 此题主要考查了一元二次方程的应用，关键是弄懂题意，找出题目中的等量关系，表示出销售量和每件利润，再列出方程．
练习册系列答案
相关题目
6．
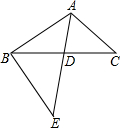如图，△ABC中，AE交BC于点D，∠C=∠E，AD=4，BC=8，BD：DC=5：3，则DE的长等于（ ）
如图，△ABC中，AE交BC于点D，∠C=∠E，AD=4，BC=8，BD：DC=5：3，则DE的长等于（ ）| A． | $\frac{20}{3}$ | B． | $\frac{17}{4}$ | C． | $\frac{16}{3}$ | D． | $\frac{15}{4}$ |
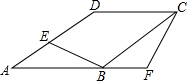如图，在菱形ABCD中，点E是边AD上一点，延长AB至点F，使BF=AE，连接BE、CF．
如图，∠1+∠2+∠3+∠4+∠5+∠6+∠7=540°．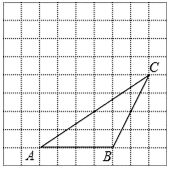
如图，△ABC的顶点都在方格纸的格点上．将△ABC向左平移2格，再向上平移4格．请在图中画出平移后的△A′B′C′，再在图中画出△A′B′C′的高C′D′、中线A′E，若S△BCP=S△ACB，P为异于点B的格点，则点P的个数为4个．