题目内容
11.在△ABC中,AB=13,BC=10,BC边上的中线AD=12,则AC=( )| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
分析 在△ABD中,根据勾股定理的逆定理即可判断AD⊥BC,然后根据线段的垂直平分线的性质,即可得到AC=AB,从而求解.
解答 解:∵AD是中线,AB=13,BC=10,
∴BD=$\frac{1}{2}$BC=5.
∵52+122=132,即BD2+AD2=AB2,
∴△ABD是直角三角形,则AD⊥BC,
又∵BD=CD,
∴AC=AB=13.
故选D.
点评 本题考查的是勾股定理的逆定理,熟知如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形是解答此题的关键.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
6.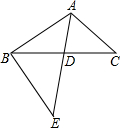 如图,△ABC中,AE交BC于点D,∠C=∠E,AD=4,BC=8,BD:DC=5:3,则DE的长等于( )
如图,△ABC中,AE交BC于点D,∠C=∠E,AD=4,BC=8,BD:DC=5:3,则DE的长等于( )
 如图,△ABC中,AE交BC于点D,∠C=∠E,AD=4,BC=8,BD:DC=5:3,则DE的长等于( )
如图,△ABC中,AE交BC于点D,∠C=∠E,AD=4,BC=8,BD:DC=5:3,则DE的长等于( )| A. | $\frac{20}{3}$ | B. | $\frac{17}{4}$ | C. | $\frac{16}{3}$ | D. | $\frac{15}{4}$ |
 如图,在同一平面内,将△ABC绕点A逆时针旋转40°到△AED的位置,恰好使得EC∥AB,则∠CAB的大小为70°.
如图,在同一平面内,将△ABC绕点A逆时针旋转40°到△AED的位置,恰好使得EC∥AB,则∠CAB的大小为70°.